
分析 (1)根据“匀称中线”的定义判断即可;
(2)由匀称三角形的定义和(1)的结论可知,匀称中线是AC边上的中线,设AC=2a,则CD=a,BD=2a,由勾股定理得BC=$\sqrt{3}$a,AB=$\sqrt{7}$a,得出结论;
(3)①根据图形旋转的性质知,将△ABC 绕点A逆时针旋转45°,即将AC,AB绕点A逆时针各旋转45°得△ADE,可得图2;
②根据图形旋转的性质知,∠DAE=∠BAC=45°,AD=AB,∠DAC=90°,△ADC是匀称三角形,由(2)的结论知,AD:AC=$2:\sqrt{3}$,AB:AC=$2:\sqrt{3}$,设AC=$\sqrt{3}$k
由等腰直角三角形的性质知,AH=CH=$\sqrt{3}$k•$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}}{2}$k,数形结合得BH,得tan∠B,由圆周角定理得∠AMC=∠B,得tan∠AMC.
解答 解:(1)根据“匀称中线”,的定义判断,
①√,②√,
故答案为:√,√.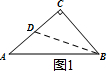
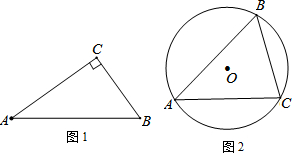
(2)如图1,∵∠C=90°,AC>BC
由(1)可知△ABC的匀称中线是AC边上的中线,设D为AC中点,则BD为匀称中线,
设AC=2a,则CD=a,BD=2a,
∵∠C=90°,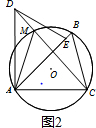
∴BC=$\sqrt{3}$a,
∴AB=$\sqrt{{(2a)}^{2}{+(\sqrt{3}a)}^{2}}$=$\sqrt{7}$a,
∴BC:AC:AB=$\sqrt{3}$:2:$\sqrt{7}$;
(3)①如图2;
②如图3,∵△ABC绕点A逆时针旋转45°得△ADE,
∴∠DAE=∠BAC=45°,AD=AB,
∴∠DAC=90°,AD>AC,
∵△ADC是匀称三角形,
∴AD:AC=$2:\sqrt{3}$,即AB:AC=$2:\sqrt{3}$,
过点C作CH⊥AB于H,则∠AHC=∠BHC=90°,
设AC=$\sqrt{3}$k,则AH=CH=$\sqrt{3}$k•$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}}{2}$k,
∴BH=2k-$\frac{\sqrt{6}}{2}k$=$\frac{4-\sqrt{6}}{2}$k,
∴tan∠B=$\frac{CH}{BH}$=$\frac{\frac{\sqrt{6}}{2}k}{\frac{4-\sqrt{6}}{2}k}$=$\frac{\sqrt{6}}{4-\sqrt{6}}$=$\frac{3+2\sqrt{6}}{5}$,
在⊙O中,由∠AMC=∠B得tan∠AMC=$\frac{3+2\sqrt{6}}{5}$.
点评 本题主要考查了旋转的性质,等腰直角三角形的性质,圆周角定理,匀称三角形的定义等,数形结合,掌握旋转的性质,理解匀称三角形的定义是解答此题的关键.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:解答题
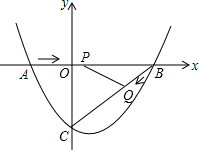 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C,tan∠BAC=2.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C,tan∠BAC=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
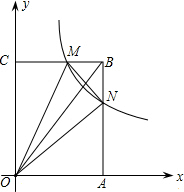 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$在第一象限的部分经过矩形OABC的中心E,分别与矩形的BC、BA边相交于M、N,△BMN的面积等于9,则k的值为8.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$在第一象限的部分经过矩形OABC的中心E,分别与矩形的BC、BA边相交于M、N,△BMN的面积等于9,则k的值为8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
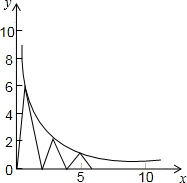 如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )| A. | $\frac{6}{2n-1}$ | B. | $\frac{6}{{2}^{n+1}}$ | C. | $\frac{6}{2n+1}$ | D. | $\frac{6}{{2}^{n-1}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
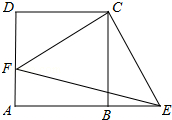 如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°.
如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°.查看答案和解析>>
科目:初中数学 来源:2016-2017学年度海南省九年级第二次月考数学试卷(解析版) 题型:解答题
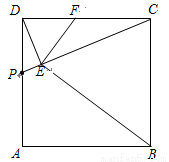
如图,正方形ABCD中,点P是AD上的一动点(与点D、点A不重合),DE⊥CP,垂足为E,EF⊥BE与DC交于点F.
(1)求证:△DEF∽△CEB;
(2)当点P运动到DA的中点时,求证:点F为DC的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com