
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,若取前3格子中的任意两个数记作![]() ,且
,且![]() ,那么所有的
,那么所有的![]() 的和可以通过计算
的和可以通过计算![]() 得到,其结果为_____,若
得到,其结果为_____,若![]() 为前
为前![]() 格子中的任意两个数,且
格子中的任意两个数,且![]() ,则所有的
,则所有的![]() 的和为_____.
的和为_____.
9 | ★ | ☆ | x | ﹣6 | 2 | …… |
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边的中点,分别过B、C做射线AD的垂线,垂足分别为E、F,连接BF、CE.
(1)求证:四边形BECF是平行四边形;
(2)我们知道S△ABD=S△ACD,若AF=FD,在不添加辅助线的条件下,直接写出与△ABD、△ACD面积相等的所有三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图
如图![]() ,在
,在![]() 中,
中,![]() ,若
,若![]() 是
是![]() 和
和![]() 的平分线交点,求
的平分线交点,求![]() 的度数。
的度数。

![]() 若是内任意一点,试探究
若是内任意一点,试探究![]() 与
与![]() 之间的关系,并说明理由
之间的关系,并说明理由

![]() 请你直接利用以上结论,解决以下问题:
请你直接利用以上结论,解决以下问题:
①图![]() 中点
中点![]() 为
为![]() 内任意一点,若
内任意一点,若![]() 则
则![]()
![]()

②如图![]() 平分
平分![]() 平分
平分![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与x轴相交于点A,与直线
与x轴相交于点A,与直线![]() 相交于点P.动点E从原点O出发,以每秒2个单位的速度沿着O→P→A的路线向点A匀速运动,同时动点F从原点O出发,以每秒2个单位的速度沿着射线OA的方向运动,当点E到达终点A时点F随即停止运动,设运动时间为t秒,当动点E、F所在的直线将△OPA的面积分成1∶2的两部分时,t的值为_________________。
相交于点P.动点E从原点O出发,以每秒2个单位的速度沿着O→P→A的路线向点A匀速运动,同时动点F从原点O出发,以每秒2个单位的速度沿着射线OA的方向运动,当点E到达终点A时点F随即停止运动,设运动时间为t秒,当动点E、F所在的直线将△OPA的面积分成1∶2的两部分时,t的值为_________________。
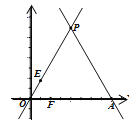
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120,△ABF为等边三角形;点E.F分别在菱形的边BC.CD上滑动,且点E.F不与点B.C.D重合,当点E.F分别在BC.CD上滑动时,求四边形ABCF的面积= ___________并求△CEF面积的最大值___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请观察下列算式,找出规律并填空
![]() =1-
=1-![]() ,
, ![]() =
=![]() -
-![]() ,
, ![]() =
=![]() -
-![]() ,
, ![]() =
=![]() -
-![]()
则第10个算式是 _____________=_____________
第n个算式是 ___________=_____________
根据以上规律解答以下三题:(1)![]()
(2)若有理数a、b满足|a-1|+![]() =0 ,试求:
=0 ,试求:
![]() +
+![]() +
+![]() + …+
+ …+![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收33万元.而该游乐设施开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数;
(1)若维修保养费用第1个月为2万元,第2个月为4万元.求y关于x的解析式;
(2)求纯收益g关于x的解析式;
(3)问设施开放几个月后,游乐场的纯收益达到最大;几个月后,能收回投资?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线p: ![]() 的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是
的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是![]() 和y=2x+2,则这条抛物线的解析式为____________________.
和y=2x+2,则这条抛物线的解析式为____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com