
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 在
在![]() 内并排
内并排![]() 不重叠
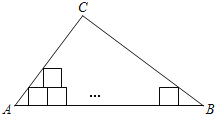
不重叠![]() 放入边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放
放入边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放![]()
![]() 个小正方形纸片.
个小正方形纸片.
A. 14个 B. 15个 C. 16个 D. 17个
【答案】C
【解析】分析:
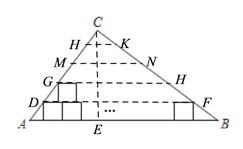
如下图,过点C作CE⊥AB于点E,则由已知条件易得CE=4.8,从而可知在△ABC内部,小正方形可以摆放4层,设这四层小正方形的上边沿所在直线分别与AC、BC相交于点D、F、G、H、M、N、K、H,则可得HK∥MN∥GH∥DF∥AB,由此结合已知条件求得DF、GH、MN、HK的长,即可知道每层可摆放的小正方形的个数,从而求得所求答案.
详解:
过点C作CE⊥AB于点E,
∵在Rt△ABC中,∠C=90°,AC=8,BC=6,
∴由勾股定理可得:AB=10,
∵S△ABC=![]() AB·CE=
AB·CE=![]() AC·BC,
AC·BC,
∴![]() ,解得CE=4.8,
,解得CE=4.8,
∴△ABC内部,小正方形可以摆放4层,
设这四层小正方形的上边沿所在直线分别与AC、BC相交于点D、F、G、H、M、N、K、H,则可得HK∥MN∥GH∥DF∥AB,
∵DF∥AB,小正方形的边长为1,
∴DF:AB=(4.8-1):4.8,解得DF=![]() ,
,
∴第一层可摆放小正方形7个,
同理可得第二层可摆放小正方形5个,第三层可摆放小正方形3个,第四层可摆放小正方形1个,
∴△ABC内部共可摆放小正方形16个.
故选C.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把数轴上表示数一1的点称为离心点,记作点Φ.对于两个不同的点M和N,若M,N两点到离心点Φ的距离相等,则称点M,N互为离心变换点,例如:如图,因为表示数一3的点M和表示数1的点N,它们与离心点重的距离都是2个单位长度,所以点M,N互为离心变换点.

(1)已知点A表示数a,点B表示数b,且点A,B互为离心变换点
①若a=-4,则b= ;若b=π,则a= ;
②用含a的式子表示b,则b= ;
③若把点A表示的数乘以3,再把所得数表示的点沿着数轴向左移动3个单位长度恰好到点B,求点A表示的数;
(2)若数轴上的点P表示数m.对点P做如下操作:点P沿数轴向右移动k(k>0)个单位长度得到P1,P2为P1的离心变换点,点P2沿数轴向右移动k个单位长度得到P3,P4为P3的离心变换点,…,依此顺序不断地重复,得到点Ps,P6,…,Pn,已知点P2019表示的数是-5,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足(a-![]() )2+
)2+![]() +
+![]() =0,
=0,
(1)求a、b、c的值.
(2)试问以a、b、c为边能否构成直角三角形?若能构成,求出直角三角形周长;若不能构成直角三角形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
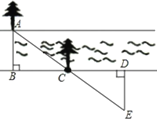
【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.
(1)河的宽度是 米.
(2)请你说明他们做法的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示,根据图象解答下列问题:
(1)洗衣机的进水时间是______分钟,清洗时洗衣机中的水量是_______升.
(2)进水时y与x之间的关系式是____________.
(3)已知洗衣机的排水速度是每分钟18升,如果排水时间为2分钟,排水结束时洗衣机中剩下的水量是____________升.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农机租赁公司共有50台收割机,其中甲型20台,乙型30台,现将这50台联合收割机派往A,B两地区收割水稻,其中30台派往A地区,20台派往B地区,两地区与该农机公司商定的每天租赁价格如表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800元 | 1600元 |
B地区 | 1600元 | 1200元 |
![]() 设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y元,求y关于x的函数关系式;
设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y元,求y关于x的函数关系式;
![]() 若使农机租赁公司这50台收割机一天所获租金不低于79600元,试写出满足条件的所有分派方案;
若使农机租赁公司这50台收割机一天所获租金不低于79600元,试写出满足条件的所有分派方案;
![]() 农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由.
农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义符号max﹛a , b﹜的含义为:当a≥b时, max﹛a , b﹜=a;当a<b时,max﹛a , b﹜=b.如 max﹛2 , -3﹜=2 , max﹛-4 , -2﹜=-2,则max﹛-x2+2x+3 , |x|﹜的最小值是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com