
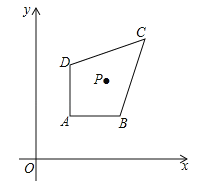
【题目】如图,在平面直角坐标系中xOy中,已知点A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),m>0,1<a<3,点P(n﹣m,n)是四边形ABCD内的一点,且△PAD与△PBC的面积相等,求n﹣m的值.
【答案】![]() .
.
【解析】
试题分析:过点P作x轴的平行线PE交BC于点E,根据点B、C的坐标利用待定系数法求出直线BC的解析式,结合点P的坐标即可得出点E的坐标,根据三角形的面积公式结合△PAD与△PBC的面积相等,即可得出关于n﹣m的一元一次方程,解方程即可得出结论.
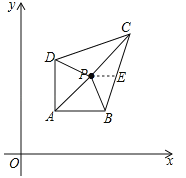
试题解析:过点P作x轴的平行线PE交BC于点E,如图所示.
设直线BC的解析式为y=kx+b,将点B(a,m+1)、C(3,m+3)代入y=kx+b中,得:![]() ,解得:
,解得: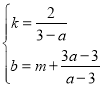 ,∴直线BC的解析式为
,∴直线BC的解析式为![]() .
.
当y=n时,x=![]() ,∴E(
,∴E(![]() ,n),PE=
,n),PE=![]() ﹣1.
﹣1.
∵A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),P(n﹣m,n),∴AD=a﹣1,∴S△PAD=![]() AD(xP﹣xA)=
AD(xP﹣xA)=![]() (a﹣1)(n﹣m﹣1),S△PBC=
(a﹣1)(n﹣m﹣1),S△PBC=![]() PE(yC﹣yB)=
PE(yC﹣yB)=![]() [
[![]() ﹣1]×2=
﹣1]×2=![]() ﹣1.
﹣1.
∵S△PAD=S△PBC,∴![]() (a﹣1)(n﹣m﹣1)=
(a﹣1)(n﹣m﹣1)=![]() ﹣1,解得:n﹣m=
﹣1,解得:n﹣m=![]() .
.


科目:初中数学 来源: 题型:
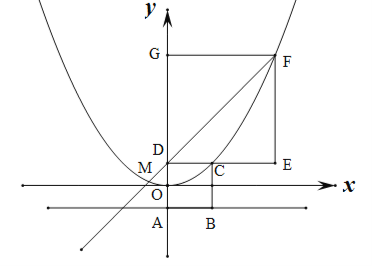
【题目】(本题满分10分)如图,在平面直角坐标系中,正方形ABCD和正方形DEFG的边长分别为![]() ,点A、D、G在
,点A、D、G在![]() 轴上,坐标原点O为AD的中点,抛物线
轴上,坐标原点O为AD的中点,抛物线![]() 过C、F两点,连接FD并延长交抛物线于点M.
过C、F两点,连接FD并延长交抛物线于点M.
(1)若![]() ,求m和b的值;
,求m和b的值;
(2)求![]() 的值;
的值;
(3)判断以FM为直径的圆与AB所在直线的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
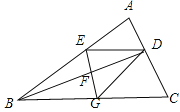
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列函数关系中,是二次函数的是( )
A.在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
B.当距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长C与边长a之间的关系
D.圆的面积S与半径R之间的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于 ![]() 的分式方程
的分式方程 ![]() =1,下列说法正确的是( )
=1,下列说法正确的是( )
A.方程的解是 ![]() =
= ![]() 3
3
B.当 ![]() >3时,方程的解是正数
>3时,方程的解是正数
C.当 ![]() <3时,方程的解为负数
<3时,方程的解为负数
D.以上答案都正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在①(-1)-3=1;②(-1)3=-3;③3a-2= ![]() ;④(-x)5÷(-x)-2=-x7中,不正确的式子有( )
;④(-x)5÷(-x)-2=-x7中,不正确的式子有( )
A.①②
B.②③
C.①②③
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个暗箱里放有a个除颜色外都完全相同的红、白、蓝三种球,其中红球有4个,白球有10个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在20%.
(1)试求出a的值;
(2)从中任意摸出一个球,下列事件:①该球是红球;②该球是白球;③该球是蓝球.试估计这三个事件发生的可能性的大小,并将三个事件按发生的可能性从小到大的顺序排列(用序号表示事件).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com