
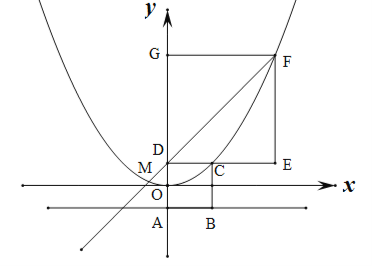
【题目】(本题满分10分)如图,在平面直角坐标系中,正方形ABCD和正方形DEFG的边长分别为![]() ,点A、D、G在
,点A、D、G在![]() 轴上,坐标原点O为AD的中点,抛物线
轴上,坐标原点O为AD的中点,抛物线![]() 过C、F两点,连接FD并延长交抛物线于点M.
过C、F两点,连接FD并延长交抛物线于点M.
(1)若![]() ,求m和b的值;
,求m和b的值;
(2)求![]() 的值;
的值;
(3)判断以FM为直径的圆与AB所在直线的位置关系,并说明理由.
【答案】(1)m=![]() ,b=1+
,b=1+![]() (2)
(2)![]() =1+
=1+![]() (3)以FM为直径的圆与AB所在的直线相切
(3)以FM为直径的圆与AB所在的直线相切
【解析】
试题分析:(1)由a代入可求C,再根据待定系数法可求得m值,然后把F点坐标代入可求b;
(2)把C(2a,a)、F(2b,2b+1)代入y=![]() 得可求得
得可求得![]() =1+
=1+![]() ;
;
(3)由C、F、D的坐标可求得m=![]() ,然后可求得用a表示的F点的坐标,求出直线MF的解析式,代入二次函数,求得M点的坐标,然后过M作x轴的平行线,过F作y轴平行线相交于点H,取MF得中点Q,做垂线QN垂直AB 与N,交MH于P.在等腰直角三角形MFH中,求得QN=
,然后可求得用a表示的F点的坐标,求出直线MF的解析式,代入二次函数,求得M点的坐标,然后过M作x轴的平行线,过F作y轴平行线相交于点H,取MF得中点Q,做垂线QN垂直AB 与N,交MH于P.在等腰直角三角形MFH中,求得QN=![]() FM,进而得出结论.
FM,进而得出结论.
试题解析:解:(1)∵a=1
∴把C(2,1)代入y=![]() 得4m=1
得4m=1
∴m=![]()
把F(2b,2b+1)代入![]() 得
得![]()
解得b=1±![]()
负值舍去,所以b=1+![]()
(2)把C(2a,a)、F(2b,2b+1)代入y=![]() 得
得
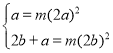
消去m得![]()
∴![]()
故![]() =1±
=1±![]()
∴![]() =1+
=1+![]()
以FM为直径的圆与AB所在的直线相切,理由如下:
C(2a,a)、F(2b,2b+1)、D(0,a)
把C(2a,a)代入y=![]() 得a=m
得a=m![]()
∴m=![]()
由(2)的结果![]() =1+
=1+![]() 可得
可得![]()
故F(2a+2![]() a,3a+2
a,3a+2![]() a)
a)
设MF:y=kx+a(k>0)
把F点坐标代入得k=1
所以MF得解析式为y=x+a
将y=x+a代入![]() ,解得x=2a±2
,解得x=2a±2![]() a
a
所以M(2a-2![]() a,3a-2
a,3a-2![]() a)
a)
过M作x轴的平行线,过F作y轴平行线相交于点H,取MF得中点Q,做垂线QN垂直AB 与N,交MH于P.
在等腰直角三角形MFH中,MH=FH=4![]() a
a
∴MF=8a
QN=2![]() a+(3a-2
a+(3a-2![]() a)+a=4a
a)+a=4a
故QN=![]() MF
MF
所以以FM为直径的圆与直线AB相切.


 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,E是AD上任意一点,延长BA到F,使得AF=AE,连接DF:
(1)旋转△ADF可得到哪个三角形?
(2)旋转中心是哪一点?旋转了多少度?
(3)BE与DF的数量关系、位置关系如何?为什么?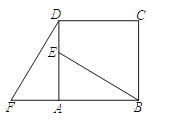
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组式的变形过程,然后回答问题: 例1: ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ﹣1.
﹣1.
例2: ![]() =
= ![]() ﹣
﹣ ![]() ,
, ![]() =
= ![]() ﹣
﹣ ![]() ,
, ![]() =
= ![]() ﹣
﹣ ![]()
利用以上结论解答以下问题:
(1)![]() =;
=; ![]() =;
=;
(2)你用含n(n为正整数)的关系式表示上述各式子的变形规律.
(3)应用上面的结论,求下列式子的值. ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]()
(4)拓展提高,求下列式子的值. ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把点P(﹣5,4)向右平移9个单位得到点P1,再将点P1绕原点逆时针旋转90°得到点P2,则点P2的坐标是( )
A.(4,﹣4)B.(4,4)C.(﹣4,﹣4)D.(﹣4,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知学校航模组设计制作的火箭模型的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则火箭升空到最高点需要的时间为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图,则符合这一结果的实验可能是( ) 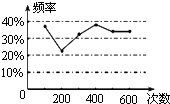
A.掷一枚正六面体的骰子,出现1点的概率
B.抛一枚硬币,出现正面的概率
C.从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
D.任意写一个整数,它能被2整除的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中xOy中,已知点A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),m>0,1<a<3,点P(n﹣m,n)是四边形ABCD内的一点,且△PAD与△PBC的面积相等,求n﹣m的值.
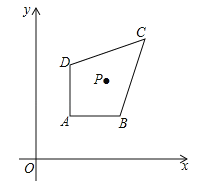
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com