
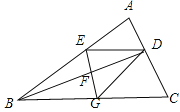
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
【答案】(1)四边形EBGD是菱形;(2)10.
【解析】
试题分析:(1)结论四边形EBGD是菱形.只要证明BE=ED=DG=GB即可.
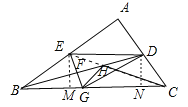
(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:∵EG垂直平分BD,∴EB=ED,GB=GD,∴∠EBD=∠EDB,∵∠EBD=∠DBC,∴∠EDF=∠GBF,在△EFD和△GFB中,∵∠EDF=∠GBF,∠EFD=∠GFB,DF=BF,∴△EFD≌△GFB,∴ED=BG,∴BE=ED=DG=GB,∴四边形EBGD是菱形.
(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=![]() ,∴EM=
,∴EM=![]() BE=
BE=![]() ,∵DE∥BC,EM⊥BC,DN⊥BC,∴EM∥DN,EM=DN=
,∵DE∥BC,EM⊥BC,DN⊥BC,∴EM∥DN,EM=DN=![]() ,MN=DE=
,MN=DE=![]() ,在RT△DNC中,∵∠DNC=90°,∠DCN=45°,∴∠NDC=∠NCD=45°,∴DN=NC=
,在RT△DNC中,∵∠DNC=90°,∠DCN=45°,∴∠NDC=∠NCD=45°,∴DN=NC=![]() ,∴MC=
,∴MC=![]() ,在RT△EMC中,∵∠EMC=90°,EM=
,在RT△EMC中,∵∠EMC=90°,EM=![]() .MC=
.MC=![]() ,∴EC=
,∴EC=![]() =
=![]() =10.
=10.
∵HG+HC=EH+HC=EC,∴HG+HC的最小值为10.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知学校航模组设计制作的火箭模型的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则火箭升空到最高点需要的时间为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图,则符合这一结果的实验可能是( ) 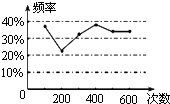
A.掷一枚正六面体的骰子,出现1点的概率
B.抛一枚硬币,出现正面的概率
C.从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
D.任意写一个整数,它能被2整除的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( ) 
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D.掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,以点B为圆心,以BC长为半径作圆,点A与该圆的位置关系为( )
A. 点A在圆外 B. 点A在圆内 C. 点A在圆上 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂第一季度的电费为 a 元,水费比电费的2倍多30元.第二季度电费比第一季度节约了30%,水费比第一季度多支出了30%.
(1)该工厂第二季度水电费(电费与水费之和)为多少元?
(2)该工厂第二季度水电费与第一季度水电费相比,是增加了还是减少了?增加或减少了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
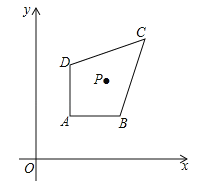
【题目】如图,在平面直角坐标系中xOy中,已知点A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),m>0,1<a<3,点P(n﹣m,n)是四边形ABCD内的一点,且△PAD与△PBC的面积相等,求n﹣m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列算式中正确的是( )
A.(-0.001)0=-1
B.(a2b5)5÷(-ab2)10=b5
C.(4x)-2= ![]()
D.
3.24×10-3=0.000324 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com