
【题目】在![]() 中,
中,![]() ,
,![]() 的垂直平分线与
的垂直平分线与![]() 所在的直线相交所得的钝角为
所在的直线相交所得的钝角为![]() ,则
,则![]() 等于_____ 度。
等于_____ 度。
【答案】70或20
【解析】
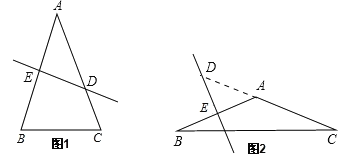
首先根据题意作图,然后由AB的垂直平分线与AC所在直线相交所得的钝角为130°,即可得∠ADE=50°,∠AED=90°,然后分两种情况讨论:
①当三角形是锐角三角形时,即可求得∠A的度数,
②当三角形是钝角三角形时,可得∠A的邻补角的度数;又由AB=AC,根据等边对等角与三角形内角和的定理,即可求得底角B的大小.
∵AB的垂直平分线与AC所在直线相交所得的钝角为130°,
即∠EDC=130°,∠ADE=50°,∠AED=90°,
①如图1,当△ABC是锐角三角形时,∠A=90°-∠ADE=90°-50°=40°.
∵AB=AC,∴∠B=∠C![]() 70°,
70°,
②如图2,当△ABC是钝角三角形时,∠BAC=∠ADE+∠AED=50°+90°=140°.
∵AB=AC,∴∠B=∠C![]() 20°.
20°.
综上所述:底角B的度数是70°或20°.
故答案为:70或20.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知:如图所示,
(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)直接写出△ABC的面积为______.
(3)在x轴上画出点P,使PA+PC最小.(不写作法,保留作图痕迹)

查看答案和解析>>
科目:初中数学 来源: 题型:
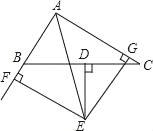
【题目】如图,在△ABC中,BC边上的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC于点G.
求证:(1)BF=CG;
(2)AB+AC=2AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点E在⊙O上,过点E的切线与AB的延长线交于点D,连接BE,过点O作BE的平行线,交⊙O于点F,交切线于点C,连接AC
(1)求证:AC是⊙O的切线;
(2)连接EF,当∠D= °时,四边形FOBE是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠CAB=∠DBA,再添加一个条件,不一定能判定△ABC≌△BAD的是( )

A. AC=BDB. ∠1=∠2C. AD=BCD. ∠C=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2)(每个小正方形的边长均为1).
(1)若点D与点A关于y轴对称则点D的坐标为 .
(2)将点B向右平移5个单位,再向上平移2个单位得到点C,则点C的坐标为 .
(3)请在图中表示出D、C两点,顺次连接ABCD,并求出A、B、C、D组成的四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠ABC=20°,外角∠ABF的平分线与CA边的延长线交于点D,外角∠EAC的平分线交BC边的延长线于点H,若∠BDA=∠DAB,则∠AHC=( )度.

A.4B.5C.6D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com