
【题目】如图,AB为⊙O的直径,点E在⊙O上,过点E的切线与AB的延长线交于点D,连接BE,过点O作BE的平行线,交⊙O于点F,交切线于点C,连接AC
(1)求证:AC是⊙O的切线;
(2)连接EF,当∠D= °时,四边形FOBE是菱形.

科目:初中数学 来源: 题型:
【题目】如图所示,有一张长为![]() 、宽为
、宽为![]() 的长方形纸片,现要在这张纸片上画两个小长方形,使小长方形的每条边都与大长方形的一边平行,并且每个小长方形的长与宽之比也都为
的长方形纸片,现要在这张纸片上画两个小长方形,使小长方形的每条边都与大长方形的一边平行,并且每个小长方形的长与宽之比也都为![]() ,然后把它们剪下,这时,所剪得的两张小长方形纸片的周长之和有最大值.求这个最大值.
,然后把它们剪下,这时,所剪得的两张小长方形纸片的周长之和有最大值.求这个最大值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图中1,![]() 分别表示甲、乙两人前往目的地所走的路程S(千米)随时间(分)变化的函数图象,以下说法:①甲比乙提前12分钟到达;②甲的平均速度为15千米/小时;③甲、乙相遇时,乙走了6千米;④乙出发6分钟后追上甲,其中正确的是( )
分别表示甲、乙两人前往目的地所走的路程S(千米)随时间(分)变化的函数图象,以下说法:①甲比乙提前12分钟到达;②甲的平均速度为15千米/小时;③甲、乙相遇时,乙走了6千米;④乙出发6分钟后追上甲,其中正确的是( )

A.①②B.③④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,等腰三角形ABC中,AB=AC,点D是BC的中点,DE⊥AB与点E、DF⊥AC与点F.求证:DE= DF;
(2)如图2,等腰三角形ABC中,AB=AC=13,BC=10,点D是BC边上的动点,DE⊥AB与点E、DF⊥AC与点F.请问DE+DF的值是否随点D位置的变化而变化?若不变,请直接写出DE+DF的值;若变化,请说明理由.
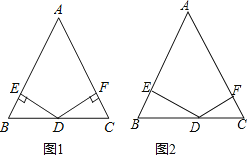
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF.
(1)试探究△A′DE的形状,请说明理由;
(2)当四边形EDD′F为菱形时,判断△A′DE与△EFC′是否全等?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年中秋节来期间,某超市以每盒80元的价格购进了1000盒月饼,第一周以每盒168元的价格销售了300盒,第二周如果单价不变,预计仍可售出300盒,该超市经理为了增加销量,决定降价,据调查,单价每降低1元,可多售出10盒,但最低每盒要赢利30元,第二周结束后,该超市将对剩余的月饼一次性赔钱甩卖,此时价格为70元/盒.
(1)若设第二周单价降低x元,则第二周的单价是 ______ ,销量是 ______ ;
(2)经两周后还剩余月饼 ______ 盒;
(3)若该超市想通过销售这批月饼获利51360元,那么第二周的单价应是多元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com