
【题目】观察图,解答下列问题.
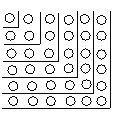
(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,……,第六层有11个圆圈.如果要你继续
下去,那么第七层有几个小圆圈?第n层呢?
(2)某一层上有77个圆圈,这是第几层?
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1 + 3 = 22.
同样,
由前三层的圆圈个数和得:1 + 3 + 5 = 32.
由前四层的圆圈个数和得:1 + 3 + 5 + 7 = 42.
由前五层的圆圈个数和得:1 + 3 + 5 + 7 + 9 = 52.
……
根据上述请你猜测,从1开始的n个连续奇数之和是多少?用公式把它表示出来.
(4)计算:1 + 3 + 5 + … + 19的和;
(5)计算:11 + 13 + 15 + … + 99的和.
【答案】(1)13个;(2n-1)个;(2)39层;(3)n2;(4)100;(5)2475.
【解析】
(1)根据已知数据即可得出每一层小圆圈个数是连续的奇数,进而得出答案;
(2)利用(1)中发现的规律得出答案即可;
(3)利用已知数据得出答案即可;
(4)利用(3)中发现的规律得出答案即可;
(5)利用(3)中发现的规律得出答案即可.
(1)第七层有13个小圆圈,第n层有(2n-1)个小圆圈,
(2)令2n-1 = 77,得,n = 39,
所以,这是第39层;
(3)1 + 3 + 5 + … +(2n-1)= n2
(4)1 + 3 + 5 + … + 19 = 102 = 100;
(5)11 + 13 + 15 + … + 99 = (1 + 3 + 5 + …… + 99)-(1 + 3 + 5 + …… + 9)= 502 -52 = 2475


科目:初中数学 来源: 题型:
【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为1,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若点P与圆心O重合,则SP为⊙O的半径长;若点P与圆心O不重合,作射线OP交⊙O于点A,则SP为线段AP的长度. 图1为点P在⊙O外的情形示意图.
(1)若点B(1,0),C(1,1), ![]() ,则SB=;SC=;SD=;
,则SB=;SC=;SD=;
(2)若直线y=x+b上存在点M,使得SM=2,求b的取值范围;
(3)已知点P,Q在x轴上,R为线段PQ上任意一点.若线段PQ上存在一点T,满足T在⊙O内且ST≥SR , 直接写出满足条件的线段PQ长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明身高为1.6米,通过地面上的一块平面镜C,刚好能看到前方大树的树梢E,此时他测得俯角为45度,然后他直接抬头观察树梢E,测得仰角为30度.求树的高度.(结果保留根号) 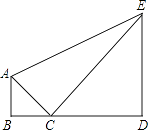
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点A(﹣6,0),B(2,0),C(0,﹣6).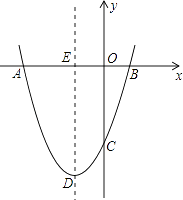
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:
13+23=1+8=9,而(1+2)2=9,∴13+23=(1+2)2;
13+23+33=36,而(1+2+3)2=36,∴13+23+33=(1+2+3)2;
13+23+33+43=100,而(1+2+3+4)2=100,∴13+23+33+43=(1+2+3+4)2;
∴13+23+33+43+53=(______ )2= ______ .
根据以上规律填空:
(1)13+23+33+…+n3=(______ )2=[ ______ ]2.
(2)猜想:113+123+133+143+153= ______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为 . 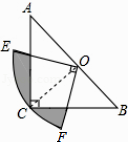
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E. 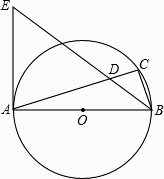
(1)∠ACB=°,理由是:;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于B,与直线y=x交于点C.
与x轴交于点A,与y轴交于B,与直线y=x交于点C.
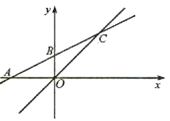
(1)求A、B、C三点的坐标;
(2)求△AOC的面积;
(3)已知点P是x轴正半轴上的一点,若△COP是等腰三角形,直接写点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com