
【题目】如图,是一张长方形纸片(其中AB∥CD),点E,F分别在边AB,AD上.把这张长方形纸片沿着EF折叠,点A落在点G处,EG交CD于点H.若∠BEH=4∠AEF,则∠CHG的度数为( )

A.108°B.120°C.136°D.144°
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,直线
,直线![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() 和点
和点![]() .
.
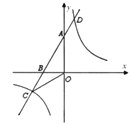
(1)求直线![]() 与反比例函数的解析式;
与反比例函数的解析式;
(2)求![]() 的度数;
的度数;
(3)将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 角(
角(![]() 为锐角),得到
为锐角),得到![]() ,当
,当![]() 为多少度时
为多少度时![]() ,并求此时线段
,并求此时线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=mx+n(m≠0,且m,n为常数)与双曲线y=![]() (k<0)在第一象限交于A,B两点,C,D是该双曲线另一支上两点,且A、B、C、D四点按顺时针顺序排列.
(k<0)在第一象限交于A,B两点,C,D是该双曲线另一支上两点,且A、B、C、D四点按顺时针顺序排列.
(1)如图,若m=﹣![]() ,n=
,n=![]() ,点B的纵坐标为
,点B的纵坐标为![]() ,
,
①求k的值;
②作线段CD,使CD∥AB且CD=AB,并简述作法;
(2)若四边形ABCD为矩形,A的坐标为(1,5),
①求m,n的值;
②点P(a,b)是双曲线y=![]() 第一象限上一动点,当S△APC≥24时,则a的取值范围是 .
第一象限上一动点,当S△APC≥24时,则a的取值范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 是
是![]() 上一动点,连接
上一动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,若要使点
,若要使点![]() 恰好在
恰好在![]() 上,则
上,则![]() 的长为().
的长为().
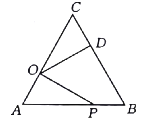
A. 4B. 5C. 6D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
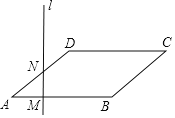
【题目】如图,点![]() 为平行四边形
为平行四边形![]() 的边
的边![]() 上一动点,过点
上一动点,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() ,且直线
,且直线![]() 与平行四边形
与平行四边形![]() 的另一边交于点
的另一边交于点![]() .当点
.当点![]() 从
从![]() 匀速运动时,设点
匀速运动时,设点![]() 的运动时间为
的运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,能大致反映
,能大致反映![]() 与
与![]() 函数关系的图象是( )
函数关系的图象是( )
A.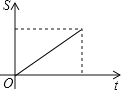 B.
B.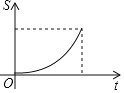
C.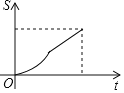 D.
D.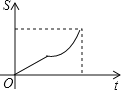
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,E为AC上一点,连接BE,将△BEC旋转,使点C落在BC上的点D处,点B落在BC上方的点F处,点E落在点C处,连接AF.求证:四边形ABDF为平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=mx+n与双曲线y=![]() 相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.
相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.
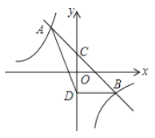
(1)求m,n的值;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)在坐标轴上是否存在异于D点的点P,使得S△PAB=S△DAB?若存在,直接写出P点坐标;若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( )
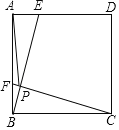
A.2B.2![]() C.4
C.4![]() ﹣2D.2
﹣2D.2![]() ﹣2
﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
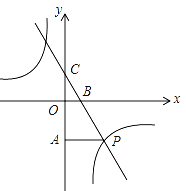
【题目】如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数![]() 的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18.
的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18.
(1)求上述一次函数与反比例函数的表达式;
(2)设Q是一次函数y=kx+3图象上的一点,且满足△OCQ的面积是△BCO面积的2倍,求出点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com