
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据二次函数的性质得二次函数y=2(x-3)2+1的开口向上,对称轴为直线x=3,抛物线的顶点坐标为(3,1);当x<3时,y随x的增大而减小;当x>3时,y随x的增大而增大,然后依次对各命题进行判断.
解答 解:抛物线y=2(x-3)2+1,
因为a>0,则抛物线开口向上,所以①错误;
抛物线的对称轴为直线x=3,所以②错误;
抛物线的顶点坐标为(3,1),所以③错误;
当x<3时,y随x的增大而减小,所以④正确.
故选D.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-$\frac{b}{2a}$时,y随x的增大而减小;x>-$\frac{b}{2a}$时,y随x的增大而增大;x=-$\frac{b}{2a}$时,y取得最小值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-$\frac{b}{2a}$时,y随x的增大而增大;x>-$\frac{b}{2a}$时,y随x的增大而减小;x=-$\frac{b}{2a}$时,y取得最大值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最高点.


科目:初中数学 来源: 题型:解答题
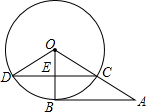 如图,A为⊙O外一点,AB切⊙O于点B,AO交⊙O于C,CD⊥OB于E,交⊙O于点D,连接OD,若AB=8,AC=4.
如图,A为⊙O外一点,AB切⊙O于点B,AO交⊙O于C,CD⊥OB于E,交⊙O于点D,连接OD,若AB=8,AC=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
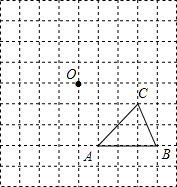 如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.
如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4}-\sqrt{2}=\sqrt{2}$ | B. | $\sqrt{8}=4\sqrt{2}$ | C. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D. | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
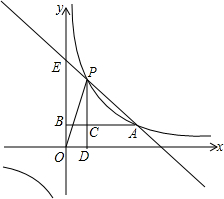 双曲线$y=\frac{k}{x}(k>0)$,点A(m,n)(m>0)在此双曲线上,过点A作AB垂直y轴交y轴于点B,点C在线段AB上,过点C作直线CD⊥x轴于点D,交此双曲线于点P.直线PA交y轴于点E.
双曲线$y=\frac{k}{x}(k>0)$,点A(m,n)(m>0)在此双曲线上,过点A作AB垂直y轴交y轴于点B,点C在线段AB上,过点C作直线CD⊥x轴于点D,交此双曲线于点P.直线PA交y轴于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 姓名 | A | B | C | D | E | F |
| 身高 | 165 | 169 | 167 | 164 | 171 | 172 |
| 身高与班级平均身高的差值 | -2 | +2 | 0 | -3 | +4 | +5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com