
已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2013年10月份的水费为620元,求该企业2013年10月份的用水量;
(3)为贯彻省委“五水共治”发展战略,鼓励企业节约用水,该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2013年收费标准收取水费外,超过80吨部分每吨另加收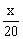 元,若某企业2014年3月份的水费和污水处理费共600元,求这个企业该月的用水量.
元,若某企业2014年3月份的水费和污水处理费共600元,求这个企业该月的用水量.
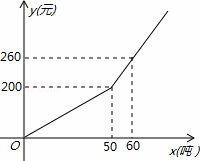
科目:初中数学 来源: 题型:
某大学生自主创业,在网上销售一种新上市的玩具,进价为20元。试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件。
(1)写出销售这种玩具每天所得的销售利润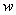 (元)与销售单价
(元)与销售单价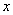 (元)之间的函数关系式
(元)之间的函数关系式
(2)求销售单价为多少元时,该玩具每天的销售利润最大。
(3)该大学生结合上述情况,提出了A、B两种营销方案。
方案A:该玩具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件玩具的利润至少为25元。
请判断哪种方案的最大利润更高,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系xOy中,已知点M0的坐标为(1,0),将线段OM0绕原点O逆时针方向旋转45°,再将其延长到M1,使得M1M0⊥OM0,得到线段OM1;又将线段OM1绕原点O逆时针方向旋转45°,再将其延长到M2,使得M2M1⊥OM1,得到线段OM2;如此下去,得到线段OM3,OM4,OM5,…
根据以上规律,请直接写出OM2014的长度为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
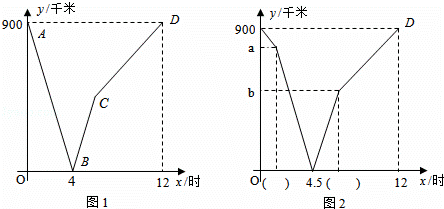
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发.不久,第二列快车也从甲地发往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分后,第二列快车与慢车相遇.设慢车行驶的时间为x(单位:时),慢车与第一、第二列快车之间的距离y(单位:千米)与x(单位:时)之间的函数关系如图1、图2,根据图象信息解答下列问题:
(1)甲、乙两地之间的距离为 千米.
(2)求图1中线段CD所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
(3)请直接在图2中的( )内填上正确的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第ts时,△EFG的面积为Scm2.


(1)当 =1s时,S的值是多少?
=1s时,S的值是多少?
(2) 当 时,点E、F、G分别在边AB、BC、CD上移动,用含t的代数式表示S;当
时,点E、F、G分别在边AB、BC、CD上移动,用含t的代数式表示S;当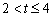 时,点E在边AB上移动,点F、G都在边CD上移动,用含t的代数式表示S.
时,点E在边AB上移动,点F、G都在边CD上移动,用含t的代数式表示S.
(3)若点F在矩形的边BC上移动,当 为何值时,以点B、E、F为顶点的三角形与以C、F、G为顶
为何值时,以点B、E、F为顶点的三角形与以C、F、G为顶 点的三角形相似?请说明理由
点的三角形相似?请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com