
����Ŀ����ͼ��Ϊ�˲�ø��в���ѧ¥�绪¥AB�ĸ߶ȣ�С���ڷ绪¥��ǰ��������㳡��F�����AB�Ķ���A������Ϊ22������������ǰ��30�����E�������¶�Ϊ3��4��̨��DE����10�����¶�D������������¥AB�ķ���ǰ��18��C������C�����A������Ϊ60����A��B��C��D��E��F��ͬһƽ���ڣ����¥AB�ĸ߶�Ϊ�� ����.�������ȷ��0.1�ף��ο����ݣ�![]() ��1.732��sin22���0.37��cos22���0.93��tan22���0.40��
��1.732��sin22���0.37��cos22���0.93��tan22���0.40��
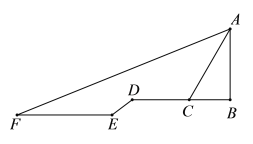
A. 10.3B. 12.3C. 20.5D. 21.3
���𰸡�D
��������
�ӳ�AB��FE���ڵ�H,����D��DG��EH�ڵ�G����BC��x���ֱ��RT��ABC��RT��DEG��RT��AHF�ɵ�BC�ij��������AB�ĸ�
��ͼ���ӳ�AB��FE���ڵ�H,����D��DG��EH�ڵ�G.
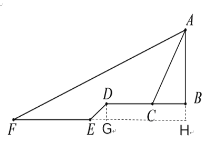
�����ı���BDGH�Ǿ��Σ�GH��BD=BC+CD.��BC��x����GH=18+x,
��RT��ABC��AB=BC��tan60��=![]() x,
x,
��RT��DEG��,DE=10,![]() =3��4
=3��4
��DG=6,EG=8
��BH=DG=6,AH=![]() x+6
x+6
FH=EF+EG+GH=30+8+18+x=56+x
��RT��AHF��,![]() =tan22��
=tan22��
��![]()
���x��12.31
��AB=![]() x=12.31��1.732��21.3
x=12.31��1.732��21.3
��ѡ��D



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�ƶ���ʱ�������� ��Զ��������У�����������ƻ���չ������A����ʷ�ݽ�������B����ʷ�ֳ���������C����ʷ֪ʶ������D����ɫ��ӽ������У��ί��ѧ����ϲ����һ�����е��飬�����ȡ�˲���ѧ�����������������Ƴ�ͼ1��ͼ2������������ͳ��ͼ������ͼ����Ϣ����������⣺
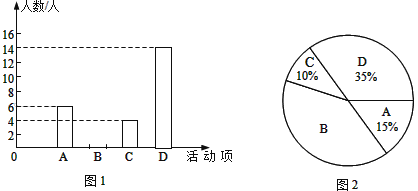
��1�����ι��������� ����ѧ����
��2����ͼ1��ͳ��ͼ����������
��3����֪�ڱ��������ϲ������ʷ֪ʶ��������Ŀ��4��ѧ����ֻ��1��Ů�����ִ���4��ѧ���������ȡ2��ѧ���μӸ���Ŀ���������û���״ͼ���б��ķ��������ǡ�ó鵽һ������һ��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������������y= ![]() ��ͼ����һ�κ���y=x+b��ͼ��
��ͼ����һ�κ���y=x+b��ͼ��
�ڵ�A��1��4������B��-4��n����

��1����һ�κ����ͷ����������Ľ���ʽ��
��2�����OAB�������
��3��ֱ��д��һ�κ���ֵ���ڷ���������ֵ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y����![]() x2+bx+c������B��2
x2+bx+c������B��2![]() ��0����C��0��2�����㣬��x�����һ������ΪA��
��0����C��0��2�����㣬��x�����һ������ΪA��
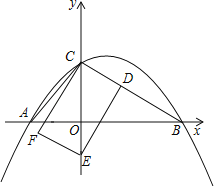
��1���������ߵĽ���ʽ��
��2����D�ӵ�C�������߶�CB��ÿ��![]() ����λ���ȵ��ٶ����B�˶�����DE��CB��y���ڵ�E����CD��DEΪ��������CDEF�����D�˶�ʱ��Ϊt��s����
����λ���ȵ��ٶ����B�˶�����DE��CB��y���ڵ�E����CD��DEΪ��������CDEF�����D�˶�ʱ��Ϊt��s����
�ٵ���F������������ʱ����t��ֵ��
������D���˶������У����ABC�����CDEF�ص����ֵ����ΪS����ֱ��д��S��t֮��ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������̬��������ֹˮ����ʧ��ij��ƻ��ڽ���������ֲ���������ּס��������ֳ�����ͬ�İ�������ɹ�ѡ����������۷������£�
���ֳ� | ���ֳ� | ||
���������� | ���۵��� | ���������� | ���۵��� |
������1000��ʱ | 4Ԫ/�� | ������2000��ʱ | 4Ԫ/�� |
����1000�õIJ��� | 3.8Ԫ/�� | ����2000�õIJ��� | 3.6Ԫ/�� |
�蹺���������x�ã��������ֳ�����������÷ֱ�Ϊy����Ԫ����y����Ԫ����
��1���ô���Ҫ����1500�ð������磬�����ڼ��ֳ������������Ϊ�� ��Ԫ�����������ֳ������������Ϊ�� ��Ԫ��
��2���ֱ����y����y����x֮��ĺ�����ϵʽ��
��3��������Ǹô�ĸ����ˣ�Ӧ��ѡ���ļ��ֳ�����������㣬Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ֱ�Ĺ�·����A��B���أ��ס�������������Ҫ��A���ͻ���B�أ��׳��ȴ�A�س���������ʻ��3Сʱ���ҳ���A�س���������ͬһ·��������ʻ�����ҳ�����B�غ����̰�ԭ�ٷ��أ��ڷ���;�еڶ�����׳��������׳�������ʱ���Ϊt (Сʱ)������֮��ľ����Ϊy��ǧ�ף���y��t�ĺ�����ϵ��ͼ��ʾ�����ҳ��ڶ�����׳�����ʱ���׳�����A��___ǧ��.
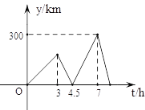
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AC��BD�ཻ�ڵ�O��BC��2OC��EΪAB����һ��.
��1����CE��6����ACE��15������BC�ij���
��2����FΪBO��һ�㣬��BF��EF��GΪCE�е㣬����FG��AG����֤��![]()
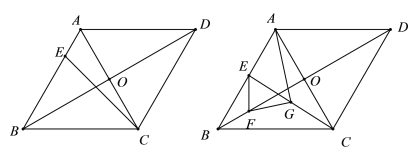
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������������y= ![]() ��ͼ����һ�κ���y=x+b��ͼ��
��ͼ����һ�κ���y=x+b��ͼ��
�ڵ�A��1��4������B��-4��n����

��1����һ�κ����ͷ����������Ľ���ʽ��
��2�����OAB�������
��3��ֱ��д��һ�κ���ֵ���ڷ���������ֵ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
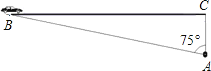
����Ŀ��������ʻ��������ͨ�¹ʵ���Ҫԭ��֮һ������ĩ��С������λͬѧ�������Լ���ѧ��֪ʶ���٣���ͼ���۲������A��������������ľ��루AC��Ϊ30������ʱ��һ��С�γ�������������ʻ����ô˳���B����ʻ��C�����õ�ʱ��Ϊ8�룬��BAC=75�㣮
��1����B��C����ľ��룻
��2�����жϴ˳��Ƿ����������60ǧ��/Сʱ�������ٶȣ�
������ʱ���뾫ȷ��1�����ο����ݣ�sin75���0.9659��cos75���0.2588��tan75���3.732��![]() ��60ǧ��/Сʱ��16.7��/�룩
��60ǧ��/Сʱ��16.7��/�룩
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com