
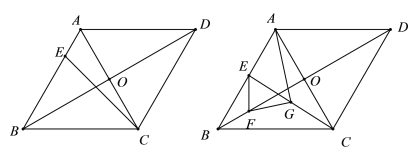
【题目】如图,在菱形ABCD中,AC,BD相交于点O,BC=2OC,E为AB边上一点.
(1)若CE=6,∠ACE=15°,求BC的长;
(2)若F为BO上一点,且BF=EF,G为CE中点,连接FG,AG,求证:![]()
【答案】(1)BC=![]() +
+![]() ;(2)见解析;
;(2)见解析;
【解析】
(1)过点E作EM⊥BC于点M,由菱形的性质和已知条件可得AB=BC=AC,进一步利用锐角三角函数解RT△CEM和RT△BEM,求出BM和CM的值,相加即可得到BC的长;
(2)延长FG至点H,使GH=FG,连接CH,AH.先证△EFG≌△CHG得到CH=BF,CH∥EF,再延长EF交BC于点K,证△AFB≌△AHC,进一步证得∠AFH=60°,最后由三角函数可得出![]() .
.
(1)过点E作EM⊥BC于点M,

∵四边形ABCD是菱形,AC与BD交于点O
∴AB=BC,AC=2CO
∵BC=2CO
∴AB=BC=AC
∴∠ACB=∠ABC=60°
∵∠ACE=15°
∴∠ECB=∠ACB—∠ACE=45°
∴CM=EM=![]() CE=
CE=![]()
∴BM=![]() EM=
EM=![]()
∴BC= CM+BM=![]() +
+![]()
(2)证明:延长FG至点H,使GH=FG,连接CH,AH.
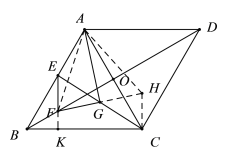
∵G为CE中点,∴EG=GC,
在△EFG与△CHG中,
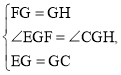 ,
,
△EFG≌△CHG(SAS),
∴EF=CH,∠CHG=∠EFG,
∴CH=BF,CH∥EF,
延长EF交BC于点K

∵菱形ABCD中,BD平分∠ABC∴∠ABF=![]() ∠ABC=30°
∠ABC=30°
∵BF=EF ∴∠BEF=∠ABF =30°
又∵∠ABC=60°∴∠EKB=90°
∵CH//EF ∴∠HCB=∠EKB=90°
∴∠ACH=∠HCB—∠ACB=90°﹣60°=30°,
∴∠ABF=∠ACH
∵BF=EF,EF=CH
∴BF=CH
在△AFB与△AHC中,

△AFB≌△AHC(SAS),
∴AF=AH,∠BAF=∠CAH
∵FG=GH,
∴AG⊥FG
∵∠BAC=∠BAF+∠FAC=60°,
∴∠CAH+∠FAC=60°,
即∠FAH=60°,
∴∠AFH=60°
∴AG=![]() FG
FG


科目:初中数学 来源: 题型:
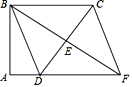
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=2,BC=6,点E是边CD的中点,连接BE并延长交AD的延长线于点F,连接CF.若△BCD是等腰三角形,则四边形BDFC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
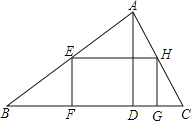
【题目】如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
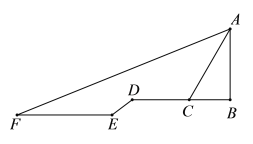
【题目】如图,为了测得高中部教学楼风华楼AB的高度,小李在风华楼正前方的升旗广场点F处测得AB的顶端A的仰角为22°,接着他往前走30米到达点E,沿着坡度为3:4的台阶DE走了10米到达坡顶D处,继续朝高楼AB的方向前行18米到C处,在C处测得A的仰角为60°,A、B、C、D、E、F在同一平面内,则高楼AB的高度为( )米.(结果精确到0.1米,参考数据:![]() ≈1.732,sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
≈1.732,sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
A. 10.3B. 12.3C. 20.5D. 21.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”
译文:“今有![]() 只雀、
只雀、![]() 只燕,分别聚焦而且用衡器称之,聚在一起的雀重,燕轻.经一只雀、一只燕交换位置而放,重量相等.
只燕,分别聚焦而且用衡器称之,聚在一起的雀重,燕轻.经一只雀、一只燕交换位置而放,重量相等.![]() 只雀、
只雀、![]() 只燕重量为
只燕重量为![]() 斤.问雀、燕每
斤.问雀、燕每![]() 只各重多少斤?”
只各重多少斤?”
请列方程组解答上面的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,管中放置着三根同样的绳子AA1、BB1、CC1.小明在左侧选两个打一个结,小红在右侧选两个打一个结,则这三根绳子能连结成一根长绳的概率为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
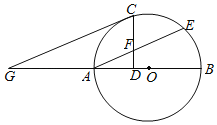
【题目】如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G.
(1)求证:CG是⊙O的切线.
(2)求证:AF=CF.
(3)若sinG=0.6,CF=4,求GA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
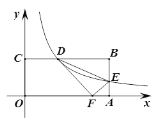
【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B 的坐标为(8,4),反比例函数y=![]() (k>0)的图象分别交边BC、AB 于点D、E,连结DE,△DEF与△DEB关于直线DE对称,当点F恰好落在线段OA上时,则k的值是________.
(k>0)的图象分别交边BC、AB 于点D、E,连结DE,△DEF与△DEB关于直线DE对称,当点F恰好落在线段OA上时,则k的值是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com