
【题目】如图,抛物线y=﹣![]() x2+bx+c经过点B(2
x2+bx+c经过点B(2![]() ,0)、C(0,2)两点,与x轴的另一个交点为A.
,0)、C(0,2)两点,与x轴的另一个交点为A.
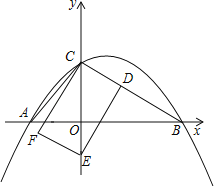
(1)求抛物线的解析式;
(2)点D从点C出发沿线段CB以每秒![]() 个单位长度的速度向点B运动,作DE⊥CB交y轴于点E,以CD、DE为边作矩形CDEF,设点D运动时间为t(s).
个单位长度的速度向点B运动,作DE⊥CB交y轴于点E,以CD、DE为边作矩形CDEF,设点D运动时间为t(s).
①当点F落在抛物线上时,求t的值;
②若点D在运动过程中,设△ABC与矩形CDEF重叠部分的面积为S,请直接写出S与t之间的函数关系式,并写出自变量t的取值范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ②
②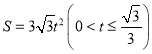 ,
,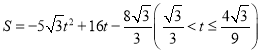 ,
,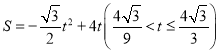
【解析】
(1)把B、C的坐标代入抛物线的解析式求解即可;
(2)①点F在抛物线上,作DG⊥y轴,FH⊥y轴,证明△CDG≌△EFH,根据全等三角形的性质有CG=HE,GD=FH,证明△CGD∽△COB,根据相似三角形的性质得到![]() 表示出OH的长度,即可求得点F的坐标,最后将点F的坐标代入抛物线的解析式求解即可;
表示出OH的长度,即可求得点F的坐标,最后将点F的坐标代入抛物线的解析式求解即可;
②当![]() 时,S=CDDE;当
时,S=CDDE;当![]() 时,S=矩形DEGF的面积-△GEH的面积.当
时,S=矩形DEGF的面积-△GEH的面积.当![]() 时,
时,![]()
解:(1)把![]() 两点代入抛物线解析式得:
两点代入抛物线解析式得:
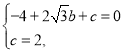
解得:![]()
则抛物线解析式为![]()
(2)①如图1所示,点F在抛物线上,作DG⊥y轴,FH⊥y轴,
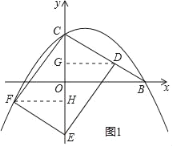
易得△CDG≌△EFH,即CG=HE,GD=FH,
由题意得:![]()
∵△CGD∽△COB,
∴![]()
即![]()
![]()
∴OH=![]() ,即
,即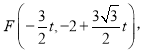
代入抛物线解析式得: ![]()
解得:t=![]() ;
;
②分三种情况考虑:
(i)如图2所示,△ABC与矩形CDEF重叠部分为矩形CDEF,
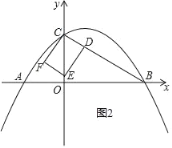
在Rt△CDE中,![]()
∴DE=3t,
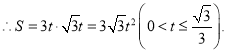
(ii)如图3所示,△ABC与矩形CDEF重叠部分为五边形CDHGF,
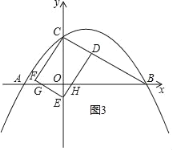
由题意得:![]()
在Rt△CED中,∠ECD=60°,
∴![]()
∴![]()
在Rt△OGE中,![]()
同理可得![]() 即
即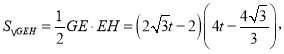
则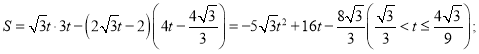
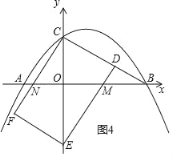
(iii)如图4,△ABC与矩形CDEF重叠部分为四边形CDMN,
由题意得: 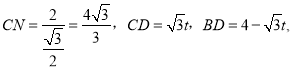
在Rt△BMD中, ![]()
则![]()
![]() ,
,
![]()
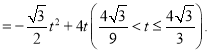


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB,AC均为⊙O的切线,切点分别为B,C,点D是优弧BC上一点,则下列关系式中,一定成立的是( )
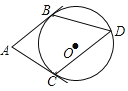
A. ∠A+∠D=180°B. ∠A+2∠D=180°
C. ∠B+∠C=270°D. ∠B+2∠C=270°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,E为矩形ABCD的边AD上一点,点P从点B出发沿折线BE-ED-DC运动到点C停止,点Q从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.若点P、点Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(![]() ),已知y与t之间的函数图象如图2所示.
),已知y与t之间的函数图象如图2所示.

给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②![]() =48
=48![]() ;③当14<t<22时,y=110-5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤△BPQ与△ABE相似时,t=14.5.
;③当14<t<22时,y=110-5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤△BPQ与△ABE相似时,t=14.5.
其中正确结论的序号是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一天,水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克,后再到水果市场去卖,已知猕猴桃和芒果当天的批发价和零售价如表所示:
品名 | 猕猴桃 | 芒果 |
批发价 | 20 | 40 |
零售价 | 26 | 50 |
![]() 他购进的猕猴桃和芒果各多少千克?
他购进的猕猴桃和芒果各多少千克?
![]() 如果猕猴桃和芒果全部卖完,他能赚多少钱?
如果猕猴桃和芒果全部卖完,他能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是_____.
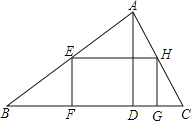
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测得高中部教学楼风华楼AB的高度,小李在风华楼正前方的升旗广场点F处测得AB的顶端A的仰角为22°,接着他往前走30米到达点E,沿着坡度为3:4的台阶DE走了10米到达坡顶D处,继续朝高楼AB的方向前行18米到C处,在C处测得A的仰角为60°,A、B、C、D、E、F在同一平面内,则高楼AB的高度为( )米.(结果精确到0.1米,参考数据:![]() ≈1.732,sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
≈1.732,sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
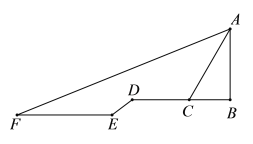
A. 10.3B. 12.3C. 20.5D. 21.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”
译文:“今有![]() 只雀、
只雀、![]() 只燕,分别聚焦而且用衡器称之,聚在一起的雀重,燕轻.经一只雀、一只燕交换位置而放,重量相等.
只燕,分别聚焦而且用衡器称之,聚在一起的雀重,燕轻.经一只雀、一只燕交换位置而放,重量相等.![]() 只雀、
只雀、![]() 只燕重量为
只燕重量为![]() 斤.问雀、燕每
斤.问雀、燕每![]() 只各重多少斤?”
只各重多少斤?”
请列方程组解答上面的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E、F分别为AB、BC、AC的中点,则下列结论:①△ADF≌△FEC;②四边形ADEF为菱形;③![]() 。其中正确的结论是____________.(填写所有正确结论的序号)
。其中正确的结论是____________.(填写所有正确结论的序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com