
【题目】如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.
求证:(1)△ABF≌△DCE;
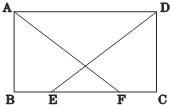
【答案】(1)∵BE=CF,BF=BE+EF,CE=CF+EF,∴BF=CE.
∵四边形ABCD是平行四边形,∴AB=DC.
在△ABF和△DCE中,∵AB=DC,BF=CE,AF=DE,
∴△ABF≌△DCE.
(2)∵△ABF≌△DCE,∴∠B=∠C.
∵四边形ABCD是平行四边形,∴AB∥CD.
∴∠B+∠C=180°.
∴∠B=∠C=90°.
∴四边形ABCD是矩形.
【解析】(1)根据等量代换得到BE=CF,根据平行四边形的性质得AB=DC.利用“SSS”得△ABF≌△DCE.
(2)平行四边形的性质得到两边平行,从而∠B+∠C=180°.利用全等得∠B=∠C,从而得到一个直角,问题得证.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
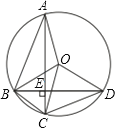
【题目】如图,在⊙O中,弦AC⊥BD于点E,连接AB,CD,BC
(1)求证:∠AOB+∠COD=180°;
(2)若AB=8,CD=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
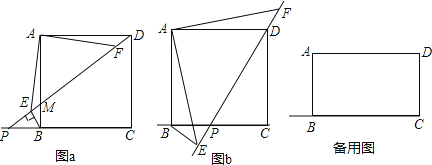
【题目】如图,正方形ABCD,点P在射线CB上运动(不包含点B、C),连接DP,交AB于点M,作BE⊥DP于点E,连接AE,作∠FAD=∠EAB,FA交DP于点F.
(1)如图a,当点P在CB的延长线上时,
①求证:DF=BE;
②请判断DE、BE、AE之间的数量关系并证明;
(2)如图b,当点P在线段BC上时,DE、BE、AE之间有怎样的数量关系?请直接写出答案,不必证明;
(3)如果将已知中的正方形ABCD换成矩形ABCD,且AD:AB=![]() :1,其他条件不变,当点P在射线CB上时,DE、BE、AE之间又有怎样的数量关系?请直接写出答案,不必证明.
:1,其他条件不变,当点P在射线CB上时,DE、BE、AE之间又有怎样的数量关系?请直接写出答案,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证:△ABP∽△BCP;
②若PA=3,PC=4,则PB= .
(2)已知锐角△ABC,分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD 相交于P点.如图(2)
①求∠CPD的度数;
②求证:P点为△ABC的费马点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c经过点B(2
x2+bx+c经过点B(2![]() ,0)、C(0,2)两点,与x轴的另一个交点为A.
,0)、C(0,2)两点,与x轴的另一个交点为A.
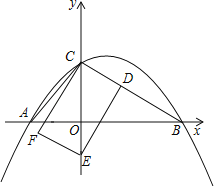
(1)求抛物线的解析式;
(2)点D从点C出发沿线段CB以每秒![]() 个单位长度的速度向点B运动,作DE⊥CB交y轴于点E,以CD、DE为边作矩形CDEF,设点D运动时间为t(s).
个单位长度的速度向点B运动,作DE⊥CB交y轴于点E,以CD、DE为边作矩形CDEF,设点D运动时间为t(s).
①当点F落在抛物线上时,求t的值;
②若点D在运动过程中,设△ABC与矩形CDEF重叠部分的面积为S,请直接写出S与t之间的函数关系式,并写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用全面调查(普查)方式的是![]()
![]()
A. 调查巴南区市民对“巴南区创建国家食品安全示范城市”的了解情况
B. 调查央视节目《国家宝藏》的收视率
C. 调查我校某班学生喜欢上数学课的情况
D. 调查学校所有电子白板的使用寿命
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B两地,甲、乙两辆货车都要从A地送货到B地,甲车先从A地出发匀速行驶,3小时后,乙车从A地出发,并沿同一路线匀速行驶,当乙车到达B地后立刻按原速返回,在返回途中第二次与甲车相遇。甲车出发的时间记为t (小时),两车之间的距离记为y(千米),y与t的函数关系如图所示,则乙车第二次与甲车相遇时,甲车距离A地___千米.
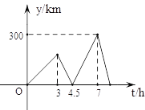
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,![]() 的顶点坐标分别是
的顶点坐标分别是![]() ,对于
,对于![]() 的横长、纵长、纵横比给出如下定义:
的横长、纵长、纵横比给出如下定义:
将![]() 中的最大值,称为
中的最大值,称为![]() 的横长,记作
的横长,记作![]() ;将
;将![]() 中的最大值,称为
中的最大值,称为![]() 的纵长,记作
的纵长,记作![]() ;将
;将![]() 叫做
叫做![]() 的纵横比,记作
的纵横比,记作![]() .
.
例如:如图![]() 的三个顶点的坐标分别是
的三个顶点的坐标分别是![]() ,则
,则![]() ,
,
所以![]() .
.
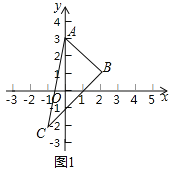
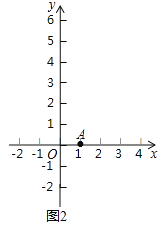
![]() 如图2,点
如图2,点![]() ,
,
![]() 点
点![]() ,
,
则![]() 的纵横比
的纵横比![]() ______
______
![]() 的纵横比
的纵横比![]() ______;
______;
![]() 点F在第四象限,若
点F在第四象限,若![]() 的纵横比为1,写出一个符合条件的点F的坐标;
的纵横比为1,写出一个符合条件的点F的坐标;
![]() 点M是双曲线
点M是双曲线![]() 上一个动点,若
上一个动点,若![]() 的纵横比为1,求点M的坐标;
的纵横比为1,求点M的坐标;
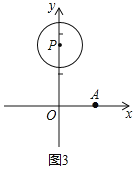
![]() 如图3,点
如图3,点![]() 以
以![]() 为圆心,1为半径,点N是
为圆心,1为半径,点N是![]() 上一个动点,直接写出
上一个动点,直接写出![]() 的纵横比
的纵横比![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为点B,反比例函数y=![]() (x>0)的图象经过AO的中点C,交AB于点D,且AD=3.
(x>0)的图象经过AO的中点C,交AB于点D,且AD=3.
(1)设点A的坐标为(4,4)则点C的坐标为 ;
(2)若点D的坐标为(4,n).
①求反比例函数y=![]() 的表达式;
的表达式;
②求经过C,D两点的直线所对应的函数解析式;
(3)在(2)的条件下,设点E是线段CD上的动点(不与点C,D重合),过点E且平行y轴的直线l与反比例函数的图象交于点F,求△OEF面积的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com