
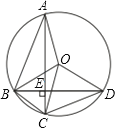
【题目】如图,在⊙O中,弦AC⊥BD于点E,连接AB,CD,BC
(1)求证:∠AOB+∠COD=180°;
(2)若AB=8,CD=6,求⊙O的直径.
【答案】(1)见解析;(2) 10
【解析】
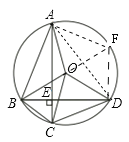
(1)延长BO交⊙O 于F,连接DF,AD,结合已知可证明AC∥DF,继而得出![]() ,从而可得∠COD=∠AOF,由∠AOB+∠AOF=180°,即可证明∠AOB+∠COD=180°;
,从而可得∠COD=∠AOF,由∠AOB+∠AOF=180°,即可证明∠AOB+∠COD=180°;
(2)连接AF,可推导得出AF=CD=6,继而根据勾股定理求出BF的长即可得.
(1)延长BO交⊙O 于F,连接DF,AD.
∵BF是直径,
∴∠BDF=90°,
∴DF⊥BD,
∵AC⊥BD,
∴AC∥DF,
∴∠CAD=∠ADF,
∴![]() ,
,
∴∠COD=∠AOF,
∵∠AOB+∠AOF=180°,
∴∠AOB+∠COD=180°;
(2)连接AF.
由(1)可知:![]() ,
,
∴AF=CD=6,
∵BF是直径,
∴∠BAF=90°,
∴BF=![]() =10,
=10,
∴⊙O的直径为10.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
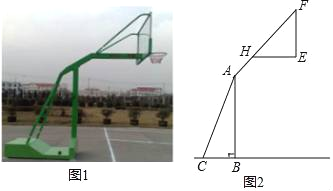
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长![]() 米,HF长
米,HF长![]() 米,HE长1米.
米,HE长1米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板底部点E到地面的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
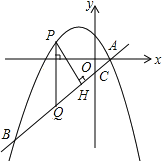
【题目】如图,在平面直角坐标系中,直线y=![]() 与抛物线y=
与抛物线y=![]() 交于A、B两点,且点A在x轴上,点B的横坐标为-4,点P为直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线交直线AB于点Q,PH⊥AB于H.
交于A、B两点,且点A在x轴上,点B的横坐标为-4,点P为直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线交直线AB于点Q,PH⊥AB于H.
(1)求b的值及sin∠PQH的值;
(2)设点P的横坐标为t,用含t的代数式表示点P到直线AB的距离PH的长,并求出PH之长的最大值以及此时t的值;
(3)连接PB,若线段PQ把△PBH分成成△PQB与△PQH的面积相等,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,CD⊥AB,∠CAB的平分线AE交CD于点H、交CB于点E,EF⊥AB于点F,则下列结论中不正确的是( )
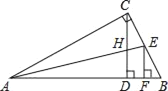
A. ∠ACD=∠BB. CH=CE=EFC. CH=HDD. AC=AF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,AC均为⊙O的切线,切点分别为B,C,点D是优弧BC上一点,则下列关系式中,一定成立的是( )
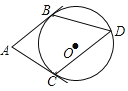
A. ∠A+∠D=180°B. ∠A+2∠D=180°
C. ∠B+∠C=270°D. ∠B+2∠C=270°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红乘坐小船往返于A、B两地,其中从A地到B地是顺流行驶.当小红第一次从A地出发时,小明同时乘坐橡皮艇从A、B之间的C地漂流而下,直至到达B地.已知A地分别距离B、C两地20千米和8千米,小船顺流速度为20千米/时,逆流速度为10千米/时,则小红、小明在途中相遇时距离C地_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.
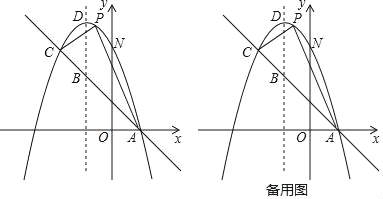
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com