
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��ABO�ı�AB��ֱ��x�ᣬ����Ϊ��B������������y��![]() (x��0)��ͼ��AO���е�C����AB�ڵ�D����AD��3��
(x��0)��ͼ��AO���е�C����AB�ڵ�D����AD��3��
(1)���A������Ϊ(4��4)���C������Ϊ�� ����
(2)����D������Ϊ(4��n)��
����������y��![]() �ı���ʽ��
�ı���ʽ��
����C��D�����ֱ������Ӧ�ĺ�������ʽ��
(3)��(2)�������£����E���߶�CD�ϵĶ���(�����C��D�غ�)������E��ƽ��y���ֱ��l�뷴����������ͼ���ڵ�F�����OEF��������ֵ��

���𰸡�(1)C(2��2)��(2)�ٷ�������������ʽΪy��![]() ����ֱ��CD�Ľ���ʽΪy����
����ֱ��CD�Ľ���ʽΪy����![]() x+3��(3)m��3ʱ��S��OEF������ֵΪ
x+3��(3)m��3ʱ��S��OEF������ֵΪ![]() .
.
��������
��1�������е����깫ʽ���ɵó����ۣ�
��2������ȷ������A���꣬�����ó���C���꣬����C��D������뷴���������м��ɵó����ۣ�
����n=1�������C��D���꣬���ô���ϵ�������ɵó����ۣ�
��3�������E���꣬������ʾ����F���꣬���ɽ��������m�ĺ�����ϵʽ���ɵó����ۣ�
(1)�ߵ�C��OA���е㣬A(4��4)��O(0��0)��
��C![]() ��
��
��C(2��2)��
�ʴ�Ϊ(2��2)��
(2)����AD��3��D(4��n)��
��A(4��n+3)��
�ߵ�C��OA���е㣬
��C(2��![]() )��
)��
�ߵ�C��D(4��n)��˫����![]() �ϣ�
�ϣ�
��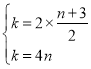 ��
��
��![]() ��
��
�෴������������ʽΪ![]() ��
��
������֪��n��1��
��C(2��2)��D(4��1)��
��ֱ��CD�Ľ���ʽΪy��ax+b��
��![]() ��
��
�� ��
��
��ֱ��CD�Ľ���ʽΪy����![]() x+3��
x+3��
(3)��ͼ����(2)֪��ֱ��CD�Ľ���ʽΪy����![]() x+3��
x+3��
���E(m����![]() m+3)��
m+3)��
��(2)֪��C(2��2)��D(4��1)��
��2��m��4��
��EF��y�ύ˫����![]() ��F��
��F��
��F(m��![]() )��
)��
��EF����![]() m+3��
m+3��![]() ��
��
��S��OEF��![]() (��
(��![]() m+3��
m+3��![]() )��m��
)��m��![]() (��
(��![]() m2+3m��4)����
m2+3m��4)����![]() (m��3)2+
(m��3)2+![]() ��
��
��2��m��4��
��m��3ʱ��S��OEF������ֵΪ![]()



 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
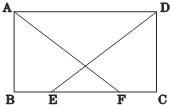
����Ŀ����ͼ����ƽ���ı���ABCD�У�E��FΪBC�����㣬��BE=CF��AF=DE��
��֤����1����ABF�ա�DCE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�ڵ�һ�����ڣ���BC��x��ƽ�У�A��B�����������ֱ�Ϊ3��1������������y��![]() ��ͼ��A��B���㣬���D������Ϊ( )
��ͼ��A��B���㣬���D������Ϊ( )
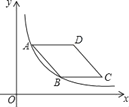
A. (2![]() ��1��3)B. (2
��1��3)B. (2![]() +1��3)
+1��3)
C. (2![]() ��1��3)D. (2
��1��3)D. (2![]() +1��3)
+1��3)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУͼ���Ϊ������ͬѧ���Ķ�����������ƻ������ס�������ͼ�鹲100�ף����м���ͼ��ÿ��120Ԫ������ͼ��ÿ��80Ԫ���蹺�����ͼ�������![]() �ף�
�ף�
��1�����ƻ���11000Ԫ�����ס�������ͼ��ʱ���ʹ�����ס�������ͼ��������ף�
��2�����������ͼ�������Ҫ����������ͼ���������![]() ����������ͼ����ܷ���Ϊ
����������ͼ����ܷ���Ϊ![]() Ԫ����������ܷ��ã�
Ԫ����������ܷ��ã�
��3��ͼ����ڲ����ӹ�������������£����ӹ������ͼ�飬Ҫ�����ͼ�������ͼ��Ĺ��������ͬ������ͼ��ÿ��100Ԫ���ܷ��ñȣ�2���������ܷ��ö��1240Ԫ����ֱ��д��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��D��E��F�ֱ�ΪAB��BC��AC���е㣬�����н��ۣ��١�ADF�ա�FEC�����ı���ADEFΪ���Σ���![]() ��������ȷ�Ľ�����____________.����д������ȷ���۵���ţ�
��������ȷ�Ľ�����____________.����д������ȷ���۵���ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����������������������ϰ�ʱ��õĽ�ͨ���ߵ�����������ȡ�����в���������е��飬Ҫ�����ߴӡ�A�����г���B���綯����C����������D����ͥ������E�����������ѡ����ѡ����õ�һ������е�������������Ƴ����²�����������ͳ��ͼ������ͳ��ͼ������ͳ��ͼ�ش��������⣺
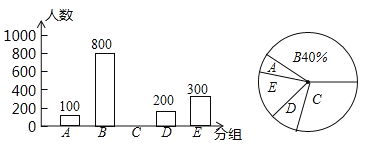
��1������ε����У�һ�������� ����������ͳ��ͼ�У�C���Ӧ������Բ�Ľ��� �㣻
��2���벹ȫ����ͳ��ͼ��
��3�����ס��������ϰ�ʱ��A��B��C��D���ֽ�ͨ���������ѡ��һ�֣���ס�������ǡ��ѡ��ͬһ�ֽ�ͨ�����ϰ�ĸ����Ƕ��٣����û���״ͼ���б�����⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
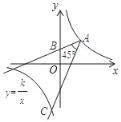
����Ŀ����ͼ��˫����![]() ������A��2��3��������AB������B��0��2����������AB��A����ʱ�뷽����ת45������˫��������C�����C�������Ϊ____.
������A��2��3��������AB������B��0��2����������AB��A����ʱ�뷽����ת45������˫��������C�����C�������Ϊ____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
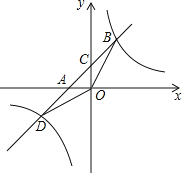
����Ŀ����֪����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��AB��x�ύ�ڵ�A(��2��0)���뷴���������ڵ�һ�����ڵ�ͼ��Ľ��ڵ�B(2��n)������BO����S��AOB��4��
(1)��÷����������Ľ���ʽ��ֱ��AB�Ľ���ʽ��
(2)��ֱ��AB��˫���ߵ���һ����ΪD�㣬���ODB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
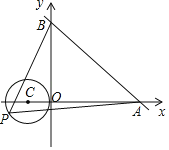
����Ŀ����ͼ��ֱ��y����![]() x+6��x�ᡢy��ֱ���A��B���㣬��P����C����1��0��ΪԲ�ģ�1Ϊ�뾶��Բ��һ�㣬����PA��PB�����PAB��������ֵΪ_____��
x+6��x�ᡢy��ֱ���A��B���㣬��P����C����1��0��ΪԲ�ģ�1Ϊ�뾶��Բ��һ�㣬����PA��PB�����PAB��������ֵΪ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com