练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．计算：
    （1）（-12）+（-13）-（-14）-（+15）+（+16）
    （2）（-$\frac{1}{4}$）-（-$\frac{5}{7}$）+（-0.75）+$\frac{2}{7}$-（+$\frac{13}{25}$）．

    分析 （1）先化简，再算加减法；
    （2）先算同分母分数，再算加减法．

    解答 解：（1）（-12）+（-13）-（-14）-（+15）+（+16）
    =-12-13+14-15+16
    =-40+30
    =-10；
    （2）（-$\frac{1}{4}$）-（-$\frac{5}{7}$）+（-0.75）+$\frac{2}{7}$-（+$\frac{13}{25}$）
    =（-$\frac{1}{4}$-0.75）+（$\frac{5}{7}$+$\frac{2}{7}$）-$\frac{13}{25}$
    =-1+1-$\frac{13}{25}$
    =-$\frac{13}{25}$．

    点评 考查了有理数加减混合运算，方法指引：①在一个式子里，有加法也有减法，根据有理数减法法则，把减法都转化成加法，并写成省略括号的和的形式． ②转化成省略括号的代数和的形式，就可以应用加法的运算律，使计算简化．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．如图所示，正方形OABC的两边OA，OC分别在x轴、y轴上，点D（5，3）在边AB上，以点C为中心，把△CDB旋转90°．
    （1）旋转后点D的对应点D′的坐标为（-2，0）或（2，10）；
    （2）求线段DD′的长；
    （3）求线段CD在旋转过程中扫过的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

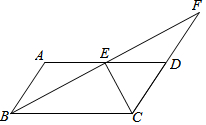    13．如图，在四边形ABCD中，AB∥CD，AD∥BC，AB=CD，AD=BC，点E是AD的中点，连接BE并延长交CD的延长线于点F．
    （1）试说明：△ABE≌△DFE；
    （2）连接CE，当BE平分∠ABC时，试说明：CE⊥BF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算
    （1）12-（-18）+（-5）-15；
    （2）-81÷$\frac{9}{4}$×（-$\frac{4}{9}$）；
    （3）1÷（$\frac{1}{6}$-$\frac{1}{3}$）×$\frac{1}{2}$； 
     （4）-14-$\frac{1}{6}$×[2-（-3）2]；
    （5）-1.57×（-0.75）+0.57×（-$\frac{3}{4}$）；
    （6）1$\frac{1}{24}$-（$\frac{3}{8}$+$\frac{1}{6}$-$\frac{3}{4}$）×24．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．计算：（-1）2016+$\sqrt{\frac{1}{4}}$+（π-3.14）0-2-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．在△ABC中，AB=AC，AD是BC边上的中线，点E是AC边上一点，且AE=$\frac{1}{3}$AC，连接BE．
    （1）如图1，连接DE，若∠ABC=60°，AC=12，求DE的长．
    （2）如图2，若点F是BE的中点，连接AF并延长交BC于点G，求证：DC=2BG．
    （3）如图3，若∠BAC=90°，过点A作AN⊥BE交BE于点M，连接DM，请直接写出DM与AB的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．计算：
    （1）3$\frac{3}{4}$-8$\frac{3}{4}$-4$\frac{1}{4}$+1.25
    （2）（$\frac{1}{2}$-$\frac{2}{3}$+$\frac{3}{4}}$）×12
    （3）9$\frac{6}{7}$×（-7）
    （4）-1+|-3|-（-2）+（-2016）×0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图①所示．以Rt△ABC的三边为直径分别作三个半圆．已知以AC为直径的半圆的面积为S1．以BC为直径的半圆的面积为S2
    （1）求以AB为直径的半圆的面积S；
    （2）如果将图中半圆改为分别以Rt△ABC的三边为斜边的等腰直角三角形，如图②所示．那么图（1）中的结论是否仍成立？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．古希腊的几何学家海伦（约公元50年）在研究中发现：如果一个三角形的三边长分别为a，b，c，那么三角形的面积S与a，b，c之间的关系式是S=$\sqrt{\frac{a+b+c}{2}•\frac{a+b-c}{2}•\frac{a+c-b}{2}•\frac{b+c-a}{2}}$①，请你举出一个例子，说明关系式①是正确的．

    查看答案和解析>>

    同步练习册答案