
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃН![]() x2ОЙ§ЕуAЃЈx1ЃЌy1ЃЉЁЂCЃЈx2ЃЌy2ЃЉЃЌЦфжаx1ЁЂx2ЪЧЗНГЬx2Љ2xЉ8ЃН0ЕФСНИљЃЌЧвx1ЃМx2ЃЌЙ§ЕуAЕФжБЯпlгыХзЮяЯпжЛгавЛИіЙЋЙВЕу
x2ОЙ§ЕуAЃЈx1ЃЌy1ЃЉЁЂCЃЈx2ЃЌy2ЃЉЃЌЦфжаx1ЁЂx2ЪЧЗНГЬx2Љ2xЉ8ЃН0ЕФСНИљЃЌЧвx1ЃМx2ЃЌЙ§ЕуAЕФжБЯпlгыХзЮяЯпжЛгавЛИіЙЋЙВЕу
ЃЈ1ЃЉЧѓAЁЂCСНЕуЕФзјБъЃЛ
ЃЈ2ЃЉЧѓжБЯпlЕФНтЮіЪНЃЛ
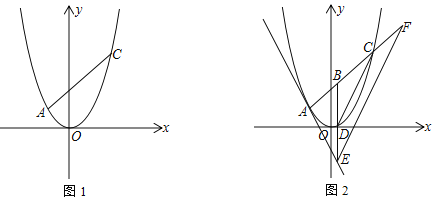
ЃЈ3ЃЉШчЭМ2ЃЌЕуBЪЧЯпЖЮACЩЯЕФЖЏЕуЃЌШєЙ§ЕуBзїyжсЕФЦНааЯпBEгыжБЯпlЯрНЛгкЕуEЃЌгыХзЮяЯпЯрНЛгкЕуDЃЌЙ§ЕуEзїDCЕФЦНааЯпEFгыжБЯпACЯрНЛгкЕуFЃЌЧѓBFЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉAЃЈЉ2ЃЌ2ЃЉЃЌCЃЈ4ЃЌ8ЃЉ ЃЈ2ЃЉyЃНЉ2xЉ2 ЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉНтвЛдЊЖўДЮЗНГЬМДПЩЕУГіЕуAЃЌCзјБъЃЛ
ЃЈ2ЃЉЯШЩшГіжБЯпlЕФНтЮіЪНЃЌдйСЊСЂХзЮяЯпНтЮіЪНЃЌгУЁїЃН0ЃЌЧѓГіkЕФжЕЃЌМДПЩЕУГіжБЯпlЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЩшГіЕуBЕФзјБъЃЌНјЖјЧѓГіBCЃЌдйБэЪОГіЕуDЃЌEЕФзјБъЃЌНјЖјЕУГіBDЃЌBEЃЌдйХаЖЯГіЁїBDCЁзЁїBEFЕУГіБШР§ЪННЈСЂЗНГЬМДПЩЧѓГіBFЃЎ
ЃЈ1ЃЉЁпx1ЁЂx2ЪЧЗНГЬx2Љ2xЉ8ЃН0ЕФСНИљЃЌЧвx1ЃМx2ЃЌ
Ёрx1ЃНЉ2ЃЌx2ЃН4ЃЌ
ЁрAЃЈЉ2ЃЌ2ЃЉЃЌCЃЈ4ЃЌ8ЃЉЃЛ
ЃЈ2ЃЉЂйЩшжБЯпlЕФНтЮіЪНЮЊyЃНkx+bЃЈkЁй0ЃЉЃЌ
ЁпAЃЈЉ2ЃЌ2ЃЉдкжБЯпlЩЯЃЌ
Ёр2ЃНЉ2k+bЃЌ
ЁрbЃН2k+2ЃЌ
ЁржБЯпlЕФНтЮіЪНЮЊyЃНkx+2k+2ЂйЃЌ
ЁпХзЮяЯпyЃН![]() x2ЂкЃЌ
x2ЂкЃЌ
СЊСЂЂйЂкЛЏМђЕУЃЌx2Љ2kxЉ4kЉ4ЃН0ЃЌ
ЁпжБЯпlгыХзЮяЯпжЛгавЛИіЙЋЙВЕуЃЌ
ЁрЁїЃНЃЈ2kЃЉ2Љ4ЃЈЉ4kЉ4ЃЉЃН4k2+16k+16ЃН4ЃЈk2+4k+4ЃЉЃН4ЃЈk+2ЃЉ2ЃН0ЃЌ
ЁрkЃНЉ2ЃЌ
ЁрbЃН2k+2ЃНЉ2ЃЌ
ЁржБЯпlЕФНтЮіЪНЮЊyЃНЉ2xЉ2ЃЛ
ЂкЦНаагкyжсЕФжБЯпКЭХзЮяЯпyЃН![]() x2жЛгавЛИіНЛЕуЃЌ
x2жЛгавЛИіНЛЕуЃЌ
ЁпжБЯпlЙ§ЕуAЃЈЉ2ЃЌ2ЃЉЃЌ
ЁржБЯпlЃКxЃНЉ2ЃЛ
ЃЈ3ЃЉгЩЃЈ1ЃЉжЊЃЌAЃЈЉ2ЃЌ2ЃЉЃЌCЃЈ4ЃЌ8ЃЉЃЌ
ЁржБЯпACЕФНтЮіЪНЮЊyЃНx+4ЃЌ
ЩшЕуBЃЈmЃЌm+4ЃЉЃЌ
ЁпЃЈ4.8ЃЉЃЌ
ЁрBCЃН![]() |mЉ4|ЃН
|mЉ4|ЃН![]() ЃЈ4ЉmЃЉ
ЃЈ4ЉmЃЉ
ЁпЙ§ЕуBзїyжсЕФЦНааЯпBEгыжБЯпlЯрНЛгкЕуEЃЌгыХзЮяЯпЯрНЛгкЕуDЃЌ
ЁрDЃЈmЃЌ![]() m2ЃЉЃЌEЃЈmЃЌЉ2mЉ2ЃЉЃЌ
m2ЃЉЃЌEЃЈmЃЌЉ2mЉ2ЃЉЃЌ
ЁрBDЃНm+4Љ![]() m2ЃЌBEЃНm+4ЉЃЈЉ2mЉ2ЃЉЃН3m+6ЃЌ
m2ЃЌBEЃНm+4ЉЃЈЉ2mЉ2ЃЉЃН3m+6ЃЌ
ЁпDCЁЮEFЃЌ
ЁрЁїBDCЁзЁїBEFЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр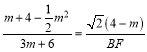 ЃЌ
ЃЌ
ЁрBFЃН6![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇЮЊСЫПМВьОХФъМЖбЇЩњЕФжаПМЬхг§ВтЪдГЩМЈЃЈТњЗж30ЗжЃЉЃЌЫцЛњГщВщСЫ40УћбЇЩњЕФГЩМЈЃЈЕЅЮЛЃКЗжЃЉЃЌЕУЕНШчЯТЕФЭГМЦЭМЂйКЭЭМЂкЃЎЧыИљОнЯрЙиаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
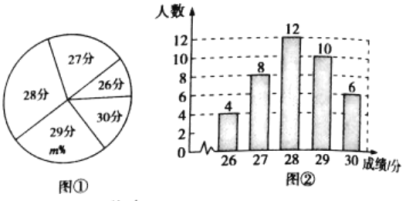
ЃЈ1ЃЉЭМжаmЕФжЕЮЊ_______________.
ЃЈ2ЃЉЧѓет40ИібљБОЪ§ОнЕФЦНОљЪ§ЁЂжкЪ§КЭжаЮЛЪ§ЃК
ЃЈ3ЃЉИљОнбљБОЪ§ОнЃЌЙРМЦИУжабЇОХФъМЖ2000УћбЇЩњжаЃЌЬхг§ВтЪдГЩМЈЕУТњЗжЕФДѓдМгаЖрЩйУћбЇЩњЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАбОиаЮжНЦЌOABCЗХШыЦНУцжБНЧзјБъЯЕжаЃЌЪЙOAЁЂOCЗжБ№ТфдкxжсЃЌyжсЩЯЃЌСЌOBЃЌНЋжНЦЌOABCбиOBелЕўЃЌЪЙЕуAТфдкAЁфЕФЮЛжУЃЌШєOB=![]() ЃЌtanЁЯBOC=
ЃЌtanЁЯBOC=![]() ЃЌдђЕуAЁфЕФзјБъЃЈЁЁЁЁЃЉ
ЃЌдђЕуAЁфЕФзјБъЃЈЁЁЁЁЃЉ

A. ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ B. ЃЈЉ
ЃЉ B. ЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉ C. ЃЈЉ
ЃЉ C. ЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉ D. ЃЈЉ
ЃЉ D. ЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
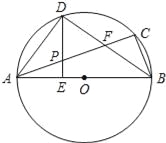
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЁїABCФкНггкЁбOЃЌABЮЊжБОЖЃЌЁЯCBAЕФЦНЗжЯпНЛACгкЕуFЃЌНЛЁбOгкЕуDЃЌDEЁЭABгкЕуEЃЌЧвНЛACгкЕуPЃЌСЌНсADЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯDAC=ЁЯDBAЃЛ
ЃЈ2ЃЉЧѓжЄЃКPЪЧЯпЖЮAFЕФжаЕуЃЛ
ЃЈ3ЃЉСЌНгCDЃЌШєCDЉ3ЃЌBDЉ4ЃЌЧѓЁбOЕФАыОЖКЭDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
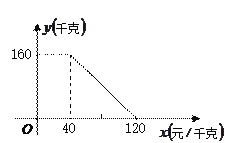
ЁОЬтФПЁПФГЩЬЕъвд40дЊ/ЧЇПЫЕФНјМлЙКНјвЛХњВшвЖЃЌОЕїВщЗЂЯжЃЌдквЛЖЮЪБМфФкЃЌЯњЪлСП![]() (ЧЇПЫ)гыЯњЪлМл
(ЧЇПЫ)гыЯњЪлМл![]() (дЊ/ЧЇПЫ)ГЩвЛДЮКЏЪ§ЙиЯЕЃЌЦфЭМЯѓШчЭМЫљЪО.
(дЊ/ЧЇПЫ)ГЩвЛДЮКЏЪ§ЙиЯЕЃЌЦфЭМЯѓШчЭМЫљЪО.
ЃЈ1ЃЉЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪН(ВЛБиаДГіздБфСП
жЎМфЕФКЏЪ§ЙиЯЕЪН(ВЛБиаДГіздБфСП![]() ЕФШЁжЕЗЖЮЇ)ЃЛ
ЕФШЁжЕЗЖЮЇ)ЃЛ
ЃЈ2ЃЉШєИУЩЬЕъЯњЪлетХњВшвЖЕФГЩБОВЛГЌЙ§2800дЊЃЌдђЫќЕФзюЕЭЯњЪлМлгІЖЈЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСРэНтЃК
ИјЖЈвЛИіОиаЮЃЌШчЙћДцдкСэвЛИіОиаЮЃЌЫќЕФжмГЄКЭУцЛ§ЗжБ№ЪЧвбжЊОиаЮЕФжмГЄКЭУцЛ§ЕФ 2 БЖЃЌдђетИіОиаЮЪЧИјЖЈОиаЮЕФЁАМгБЖЁБОиаЮЃЎШчЭМЃЌОиаЮ A1B1C1D1ЪЧОиаЮ ABCD ЕФЁАМгБЖЁБОиаЮЃЎЧыФуНтОіЯТСаЮЪЬтЃК
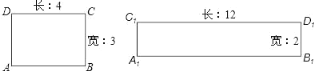
ЃЈ1ЃЉБпГЄЮЊ a ЕФе§ЗНаЮДцдкЁАМгБЖЁБе§ЗНаЮТ№ЃПШчЙћДцдкЃЌЧѓГіЁАМгБЖЁБе§ЗНаЮЕФБпГЄЃЛШчЙћВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃЈ2ЃЉЕБОиаЮЕФГЄКЭПэЗжБ№ЮЊ mЃЌn ЪБЃЌЫќЪЧЗёДцдкЁАМгБЖЁБОиаЮЃПЧызїГіХаЖЯЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУївЊЭГМЦаЁЧј500ЛЇОгУёУПдТЖЊЦњЫмСЯДќЕФЪ§СПЧщПіЃЌЫћЫцЛњЕїВщСЫЦфжа40ЛЇОгУёЃЌАДУПдТЖЊЦњЕФЫмСЯДќЕФЪ§СПЗжзщНјааЭГМЦЃЌВЂЛцжЦСЫШчЯТЕФЦЕЪ§ЗжВМБэКЭЦЕЪ§ЗжВМжБЗНЭМЃК
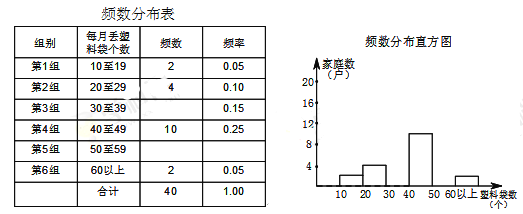
ИљОнвдЩЯЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉВЙШЋЦЕЪ§ЗжВМБэКЭЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ2ЃЉет40ЛЇМвЭЅУПдТЖЊЦњЫмСЯДќЪ§ЕФжаЮЛЪ§ЮЛгкЕк зщЃЛ
ЃЈ3ЃЉЧыФуЙРЫуИУаЁЧјУПдТЖЊЦњЫмСЯДќЕФЪ§ВЛЩйгк40ИіЕФЛЇЪ§ДѓдМга __ ЛЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌEЁЂFЗжБ№ЪЧCBЃЌABЕФжаЕуЃЌСЌНгCFВЂбгГЄЃЌгыDAЕФбгГЄЯпНЛгкЕуMЃЌСЌНгDEНЛCFгкЕуPЃЌСЌНгAPЃЌдђгаЯТСаНсТлЃКЂйЁЯBCFЃНЁЯCDEЃЛЂкAPЃНADЃКЂлCMЃНCD+DEЃЛЂмSЁїCDMЃН5SЫФБпаЮEPFBЃЌЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉ
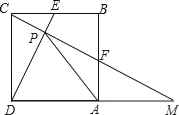
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХОМУЫЎЦНЕФВЛЖЯЬсЩ§ЃЌдНРДдНЖрЕФШЫбЁдёЕНЕчгАдКШЅЙлПДЕчгАЃЌЬхбщЪгОѕЪЂбчЃЌВЂЧвИќЖрЕФШЫЭЈЙ§ЬдЦБЦБЃЌУЈблЕШЭјЩЯЦНЬЈЙКЦБЃЌПьНнЧвЯэЪмИќЖргХЛнЃЌЕчгАЦБМлИёвВдНРДдНБувЫЃЎ2018ФъДгЭјЩЯЦНЬЈЙКТђ5еХЕчгАЦБЕФЗбгУБШдкЯжГЁЙКТђ3еХЕчгАЦБЕФЗбгУЩй10дЊЃЌДгЭјЩЯЦНЬЈЙКТђ4еХЕчгАЦБЕФЗбгУКЭЯжГЁЙКТђ2еХЕчгАЦБЕФЗбгУЙВЮЊ190дЊЃЎ
ЃЈ1ЃЉЧыЮЪ2018ФъдкЭјЩЯЦНЬЈЙКЦБКЭЯжГЁЙКЦБЕФУПеХЕчгАЦБЕФМлИёИїЮЊЖрЩйдЊЃП
ЃЈ2ЃЉ2019ФъЁАдЊЕЉЁБЕБЬьЃЌФЯЦКЩЯКЃГЧЕФЁАЛЊвъажЕмгАдКЁБАДее2018ФъдкЭјЩЯЦНЬЈЙКЦБКЭЯжГЁЙКЦБЕФЕчгАЦБЕФМлИёНјааЯњЪлЃЌЕБЬьЭјЩЯКЭЯжГЁЪлГіЕчгАЦБзмЦБЪ§ЮЊ600еХЃЎЁАдЊЕЉЁБМйЦкИеЙ§ЃЌЙлгАШЫЪ§ГіЯжЯТНЕЃЌгкЪЧИУгАдКОіЖЈНЋ1дТ2ШеЕФЯжГЁЙКЦБЕФМлИёЯТЕїЃЌЭјЩЯЙКЦБМлИёБЃГжВЛБфЃЌНсЙћЗЂЯжЯжГЁЙКЦБУПеХЕчгАЦБЕФМлИёУПНЕМл0.5дЊЃЌдђЕБЬьзмЦБЪ§БШЁАдЊЕЉЁБЕБЬьзмЦБЪ§діМг4еХЃЌОЭГМЦЃЌ1дТ2ШеЕФзмЦБЪ§жага![]() ЭЈЙ§ЭјЩЯЦНЬЈЪлГіЃЌЦфгрОљгЩЕчгАдКЯжГЁЪлГіЃЌЧвЕБЬьЦБЗПзмЪевцЮЊ19800дЊЃЌЧыЮЪИУЕчгАдКдк1дТ2ШеЕБЬьЯжГЁЙКЦБУПеХЕчгАЦБЕФМлИёЯТЕїСЫЖрЩйдЊЃП
ЭЈЙ§ЭјЩЯЦНЬЈЪлГіЃЌЦфгрОљгЩЕчгАдКЯжГЁЪлГіЃЌЧвЕБЬьЦБЗПзмЪевцЮЊ19800дЊЃЌЧыЮЪИУЕчгАдКдк1дТ2ШеЕБЬьЯжГЁЙКЦБУПеХЕчгАЦБЕФМлИёЯТЕїСЫЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com