练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．已知?ABCD，给出下列条件：①AC=BD；②∠BAD=90°；③AB=BC；④AC⊥BD，添加其中之一能使□ABCD成为菱形的条件是（　　）
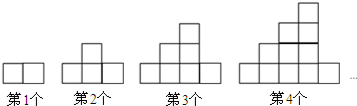
    A．①③B．②③C．③④D．①②③

    分析 四边形ABCD是平行四边形，要是其成为菱形，加上一组邻边相等或对角线垂直均可．

    解答 解：∵四边形ABCD是平行四边形，
    ①若AC=BD，可得四边形ABCD是矩形，故①错误，
    ②中∠BAD=90°，得到一矩形，不是菱形，所以②错误，
    ③中一组邻边相等，也可得到一菱形，所以③成立，
    ④若AC⊥BD，则可得其为菱形，④成立，
    故选：C．

    点评 此题考查了菱形的判定，即对角线互相垂直的平行四边形是菱形，有一组邻边相等的平行四边形是菱形，需熟练掌握菱形的两个基本判定．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    15．下列图案均是长度相同的火柴按一定的规律拼搭而成：第1个图案需7根火柴，第2个图案需13根火柴，…，依此规律，第10个图案需133根火柴．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

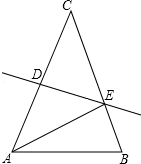    16．如图，在三角形纸片△ABC中，AC=BC，∠B=70°，将△ABC沿线段DE所在直线对折，使点A、点C重合，连接AE，则∠AED的度数是50度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

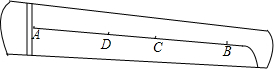    13．如图，乐器上的一根弦AB=80cm，两个端点A、B固定在乐器板面上，支撑点C是靠近点B的黄金分割点，支撑点D是靠近点A的黄金分割点，求C、D之间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．计算
    （1）$\frac{1}{2}+（{-\frac{2}{3}}）+\frac{4}{7}+（{-\frac{1}{2}}）+（{-\frac{1}{3}}）$
    （2）$（{-6.5}）+（{-2}）÷（{-\frac{2}{5}}）÷（{-5}）$
    （3）$|{9\frac{5}{19}-13\frac{3}{26}}|+5\frac{23}{26}-7\frac{14}{19}$
    （4）$-24×（{\frac{1}{2}+\frac{2}{3}-\frac{5}{6}}）$
    （5）$-{1^4}-（{1-0.5}）×\frac{1}{3}×[{2-{{（{-3}）}^2}}]$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．为了了解某校八年级1000名学生的身高，从中抽取了50名学生并对他们的身高进行统计分析，以下说法正确的是（　　）
    A．1 000名学生是总体
    B．抽取的50名学生是样本容量
    C．每位学生的身高是个体
    D．被抽取的50名学生是总体的一个样本

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．2016年扬州体育中考现场考试内容有两项，50米跑为必考项目，另在立定跳远、坐位体前屈、实心球和一分钟跳绳中选一项测试．王老师对参加体育中考的九（1）班40名学生的一项选测科目作了统计，列出如图所示的统计表，则本班参加坐位体前屈的人数是14人．
    组别立定跳远坐位体前屈实心球一分钟跳绳
    频率0.40.350.10.15

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

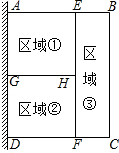    14．如图，某小区准备用篱笆围成一块矩形花圃ABCD，为了节省篱笆，一边利用足够长的墙，另外三边用篱笆围着，再用两段篱笆EF与GH将矩形ABCD分割成①②③三块矩形区域，而且这三块矩形区域的面积相等，现有总长80m的篱笆，当围成的花圃ABCD的面积最大时，AB的长为15m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

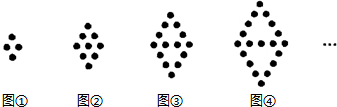
    15．如图都是由同样大小的黑棋子按一定规律摆出的图案，第①个图案有4个黑棋子，第②个图案有9个黑棋子，第③个图案有14个黑棋子，…．依次规律，第n个图案有5n-1个黑棋子．（用含n的代数式表示）

    查看答案和解析>>

    同步练习册答案