
分析 (1)原式结合后,相加即可得到结果;
(2)原式先计算除法运算,再计算加减运算即可得到结果;
(3)原式利用绝对值的代数意义化简,计算即可得到结果;
(4)原式利用乘法分配律计算即可得到结果;
(5)原式先计算乘方及绝对值运算,再计算乘法运算,最后算加减运算即可得到结果.
解答 解:(1)原式=($\frac{1}{2}$-$\frac{1}{2}$)+(-$\frac{2}{3}$-$\frac{1}{3}$)+$\frac{4}{7}$=-1+$\frac{4}{7}$=-$\frac{3}{7}$;
(2)原式=-6.5-2×$\frac{5}{2}$×$\frac{1}{5}$=-6.5-1=-7.5;
(3)原式=-9$\frac{5}{19}$-7$\frac{14}{19}$+13$\frac{3}{26}$+5$\frac{23}{26}$=-17+19=2;
(4)原式=-12-16+20=-10;
(5)原式=-1-$\frac{1}{2}$×$\frac{1}{3}$×(-7)=-1+$\frac{7}{6}$=$\frac{1}{6}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
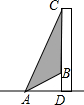 如图,某高楼CD与处地面垂直,要在高楼前的地面A处安装某种射灯,安装后,射灯发出的光线与地面的最大夹角∠DAC为70°,光线与地面的最小夹角∠DAB为35°,要使射灯发光时照射在高楼上的区域宽BC为50米,求A处到高楼的距离AD.(结果精确到0.1米)
如图,某高楼CD与处地面垂直,要在高楼前的地面A处安装某种射灯,安装后,射灯发出的光线与地面的最大夹角∠DAC为70°,光线与地面的最小夹角∠DAB为35°,要使射灯发光时照射在高楼上的区域宽BC为50米,求A处到高楼的距离AD.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,E是BC上的一点,BE=$\frac{1}{3}$BC,F是DC的中点,连接AE,EF.
如图,在正方形ABCD中,E是BC上的一点,BE=$\frac{1}{3}$BC,F是DC的中点,连接AE,EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
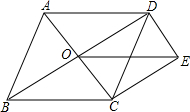 如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.
如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ③④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
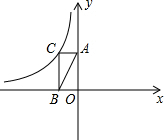 在△ABC中,∠ACB=90°,将Rt△ABC放在如图所示的平面直角坐标系中,△ABC的边AC∥x轴,AC=1,点B在x轴上,点C在函数y=-$\frac{2}{x}$(x<0)的图象上.先将此三角形作关于原点O的对称图形,再向右平移3个单位长度得到△A1B1C1,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,B1C1与此图象交于点P,则点P的纵坐标是( )
在△ABC中,∠ACB=90°,将Rt△ABC放在如图所示的平面直角坐标系中,△ABC的边AC∥x轴,AC=1,点B在x轴上,点C在函数y=-$\frac{2}{x}$(x<0)的图象上.先将此三角形作关于原点O的对称图形,再向右平移3个单位长度得到△A1B1C1,此时点A1在函数y=$\frac{k}{x}$(x>0)的图象上,B1C1与此图象交于点P,则点P的纵坐标是( )| A. | -$\frac{5}{3}$ | B. | -$\frac{3}{4}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 类比思想 | B. | 转化思想 | C. | 方程思想 | D. | 函数思想 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com