
【题目】跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系, 设此抛物线的解析式为y=ax2+bx+0.9.
(1)求该抛物线的解析式;
(2)如果小华站在OD之间,且离点O的距离为3米,当绳子甩到最高处时刚好通过他的头顶,请你算出小华的身高;
(3)如果身高为1.4米的小丽站在OD之间,且离点O的距离为t米, 绳子甩到最高处时超过她的头顶,请结合图像,写出t的取值范围 .

【答案】(1)抛物线的解析式是y=﹣0.1x2+0.6x+0.9;(2)小华的身高是1.8米;(3)1<t<5.
【解析】
试题分析:(1)已知抛物线解析式,求其中的待定系数,选定抛物线上两点E(1,1.4),B(6,0.9)坐标代入即可;
(2)小华站在OD之间,且离点O的距离为3米,即OF=3,求当x=3时,函数值;
(3)实质上就是求y=1.4时,对应的x的两个值,就是t的取值范围.
试题解析:(1)由题意得点E(1,1.4),B(6,0.9),代入y=ax2+bx+0.9得![]() ,
,
解得![]() ,
,
∴所求的抛物线的解析式是y=﹣0.1x2+0.6x+0.9;
(2)把x=3代入y=﹣0.1x2+0.6x+0.9得
y=﹣0.1×32+0.6×3+0.9=1.8
∴小华的身高是1.8米;
(3)当y=1.4时,﹣0.1x2+0.6x+0.9=1.4,
解得x1=1,x2=5,
∴1<t<5.
考点:二次函数的应用.


科目:初中数学 来源: 题型:
【题目】某中学库存若干套桌椅,准备修理后支援贫困山区学校。现有甲、乙两木工组,甲每天修理桌椅16套,乙每天修桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲组80元修理费,付乙组120元修理费。
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a、由甲单独修理;b、由乙单独修理;c、甲、乙合作同时修理。你认为哪种方案省时又省钱?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
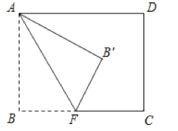
【题目】如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠。当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)小河的同旁有甲、乙两个村庄(左图),现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题。(保留作图痕迹)
①如果要求水泵站到甲、乙两村庄的距离相等,水泵站M应建在河岸AB上的何处?
②如果要求建造水泵站,供水管道使用建材最省,水泵站N又应建在河岸AB上的何处?

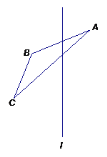
(2)如图,作出△ABC关于直线l的对称图形;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分(满分为10分):
方案①:所有评委所给分的平均数;
方案②:在所有评委所给分中,去掉一个最高分和一个最低分,然后再计算其余给分的平均数;
方案③:所有评委所给分的中位数;
方案④:所有评委所给分的众数。
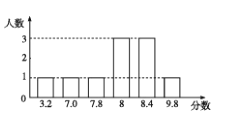
为了探究上述方案的合理性,先地某个同学的演讲成绩进行了统计实验,如图是这个同学的得分统计图。
(1)分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分,并说明你的理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=30cm,BC=40cm.点P从点A出发,以5cm/s的速度沿AC向终点C匀速移动.过点P作PQ⊥AB,垂足为点Q,以PQ为边作正方形PQMN,点M在AB边上,连接CN.设点P移动的时间为t(s).

(1)PQ=______;(用含t的代数式表示)
(2)当点N分别满足下列条件时,求出相应的t的值;①点C,N,M在同一条直线上;②点N落在BC边上;
(3)当△PCN为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
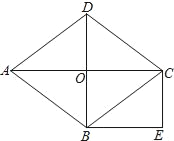
【题目】如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
(2)求四边形OBEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)该玩具销售单价定为多少元时,商场能获得12000元的销售利润?
(2)该玩具销售单价定为多少元时,商场获得的销售利润最大?最大利润是多少?
(3)若玩具厂规定该品牌玩具销售单价不低于46元,且商场要完成不少于500件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com