
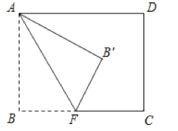
【题目】如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠。当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为___.
【答案】2![]() 或93
或93![]() .
.
【解析】
分两种情况考虑:B′在横对称轴上与B′在竖对称轴上,分别求出BF的长即可.
当B′在横对称轴上,此时AE=EB=3,如图1所示,
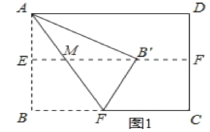
由折叠可得△ABF≌△AB′F
∴∠AFB=∠AFB′,AB=AB′=6,BF=B′F,
∴∠B′MF=∠B′FM,
∴B′M=B′F,
∵EB′∥BF,且E为AB中点,
∴M为AF中点,即EM为中位线,∠B′MF=∠MFB,
∴EM=![]() BF,
BF,
设BF=x,则有B′M=B′F=BF=x,EM=![]() x,即EB′=
x,即EB′=![]() x,
x,
在Rt△AEB′中,根据勾股定理得:3![]() +(
+(![]() x)
x) ![]() =6
=6![]() ,
,
解得:x=2![]() ,即BF=2
,即BF=2![]() ;
;
当B′在竖对称轴上时,此时AM=MD=BN=CN=4,如图2所示:

设BF=x,B′N=y,则有FN=4x,
在Rt△FNB′中,根据勾股定理得:y![]() +(4x)
+(4x) ![]() =x
=x![]() ,
,
∵∠AB′F=90°,
∴∠AB′M+∠NB′F=90°,
∵∠B′FN+∠NB′F=90°,
∴∠B′FN=∠AB′M,
∵∠AMB′=∠B′NF=90°,
∴△AMB′∽△B′NF,
∴![]() ,即
,即![]() ,
,
∴y=![]() x,
x,
∴(![]() x)
x) ![]() +(4x)
+(4x) ![]() =x
=x![]() ,
,
解得x![]() =9+3
=9+3![]() ,x
,x![]() =93
=93![]() ,
,
∵9+3![]() >4,舍去,
>4,舍去,
∴x=93![]()
所以BF的长为2![]() 或93
或93![]() ,
,
故答案为:2![]() 或93
或93![]() .
.


科目:初中数学 来源: 题型:
【题目】某天早上,一辆交通巡逻车从A地出发,在东西向的马路上巡视,中午到达B地,如果规定向东行驶为正,向西行驶为负,行驶纪录如下:(单位:km)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
+15 | -8 | +6 | +12 | -4 | +5 | -10 |
(1)B地在A地哪个方向,与A地相距多少千米?
(2)巡逻车在巡逻过程中,离开A地最远是多少千米?
(3)若每km耗油0.1升,问共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
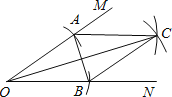
【题目】如图,在∠MON的两边上分别截取OA、OB,使OA=OB;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C,连接AC、BC、AB、OC.若AB=2cm,四边形OACB的周长为8cm.则OC的长为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区2014年投入教育经费2900万元,2016年投入教育经费3509万元.
(1)求2014年至2016年该地区投入教育经费的年平均增长率;
(2)按照义务教育法规定,教育经费的投入不低于国民生产总值的百分之四,结合该地区国民生产总值的增长情况,该地区到2018年需投入教育经费4250万元,如果按(1)中教育经费投入的增长率,到2018年该地区投入的教育经费是否能达到4250万元?请说明理由.
(参考数据: ![]() =1.1,
=1.1, ![]() =1.2,
=1.2, ![]() =1.3,
=1.3, ![]() =1.4)
=1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
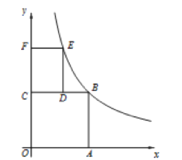
【题目】如图,正方形OABC的边OA,OC在坐标轴上,矩形CDEF的边CD在CB上,且5CD=3CB,边CF在轴上,且CF=2OC-3,反比例函数y=![]() (k>0)的图象经过点B,E,则点E的坐标是____
(k>0)的图象经过点B,E,则点E的坐标是____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
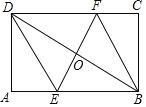
(1)求证:四边形BEDF是平行四边形;(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AM是中线,AD是高线.
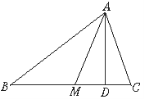
(1)若AB比AC长4 cm,则△ABM的周长比△ACM的周长多__________ cm.
(2)若△AMC的面积为12 cm2,则△ABC的面积为__________cm 2.
(3)若AD又是△AMC的角平分线,∠AMB=130°,求∠ACB的度数.(写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系, 设此抛物线的解析式为y=ax2+bx+0.9.
(1)求该抛物线的解析式;
(2)如果小华站在OD之间,且离点O的距离为3米,当绳子甩到最高处时刚好通过他的头顶,请你算出小华的身高;
(3)如果身高为1.4米的小丽站在OD之间,且离点O的距离为t米, 绳子甩到最高处时超过她的头顶,请结合图像,写出t的取值范围 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com