
【题目】已知:如图,四边形ABCD是矩形,过点D作DF∥AC交BA的延长线于点F.
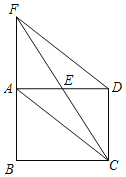
(1)求证:四边形ACDF是平行四边形;
(2)若AB=3,DF=5,求△AEC的面积.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
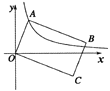
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]() 在第一象限图像上的一个动点,连接
在第一象限图像上的一个动点,连接![]() ,以
,以![]() 为长,
为长,![]() 为宽作矩形
为宽作矩形![]() ,且点
,且点![]() 在第四象限,随着点
在第四象限,随着点![]() 的运动,点
的运动,点![]() 也随之运动,但点
也随之运动,但点![]() 始终在反比例函数
始终在反比例函数![]() 的图像上,则
的图像上,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O半径为4cm,AE=6cm,求∠ADE的正切值.

查看答案和解析>>
科目:初中数学 来源: 题型:
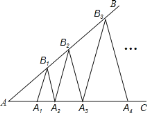
【题目】 已知∠BAC=36°,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是顶角为36°的等腰三角形,即∠A1B1A2=∠A2B2A3=∠A3B3A4=…=∠AnBnAn+1=36°,点A1,A2,A3,…,An在射线AC上,点B1,B2,B3,…,Bn在射线AB上,若A1A2=1,则线段A2018A2019的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点D是直线AB上一动点(不包含点A,B),过点B作BE⊥CD于点E,连接EA.

(1)如图1,当点D在线段AB上时,直接写出线段CE,BE,AE的数量关系:______.
(2)如图2,当点D在线段AB的延长线上时,判断线段CE,BE,AE的数量关系,并加以证明.
(3)如图3,当点D在线段BA的延长线上时,并将已知条件中的“AB=AC”改成;![]() ,其他条件不变,若CE=1,
,其他条件不变,若CE=1,![]() ,请直接写出线段BE的长.
,请直接写出线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
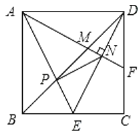
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则以下结论中:①F为CD的中点;②3AM=2DE;③tan∠EAF=![]() ;④
;④![]() ;⑤△PMN∽△DPE,正确的结论个数是( )
;⑤△PMN∽△DPE,正确的结论个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨![]() .据统计,淡季该公司平均每天有
.据统计,淡季该公司平均每天有![]() 辆货车未出租,日租金总收入为
辆货车未出租,日租金总收入为![]() 元;旺季所有的货车每天能全部租出,日租金总收入为
元;旺季所有的货车每天能全部租出,日租金总收入为![]() 元.
元.
(1)该出租公司这批对外出租的货车共有多少辆?淡季每辆货车的日租金多少元?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨![]() 元,每天租出去的货车就会减少
元,每天租出去的货车就会减少![]() 辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
查看答案和解析>>
科目:初中数学 来源: 题型:
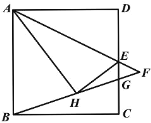
【题目】如图,在正方形ABCD中,AB=2,点E是CD的中点,连接AE,将△ADE沿AE折叠至△AHE,连接BH,延长AE,BH交于点F;BF,CD交于点G,则FG=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款![]() 元用来代理品牌服装的销售.已知该品牌服装进价每件
元用来代理品牌服装的销售.已知该品牌服装进价每件![]() 元,日销售
元,日销售![]() (件)与销售价
(件)与销售价![]() (元/件)之间的关系如图所示(实线),每天付员工的工资每人每天
(元/件)之间的关系如图所示(实线),每天付员工的工资每人每天![]() 元,每天应支付其它费用
元,每天应支付其它费用![]() 元.
元.

![]() 求日销售
求日销售![]() (件)与销售价
(件)与销售价![]() (元/件)之间的函数关系式;
(元/件)之间的函数关系式;
![]() 若暂不考虑还贷,当某天的销售价为
若暂不考虑还贷,当某天的销售价为![]() 元/件时,收支恰好平衡(收入
元/件时,收支恰好平衡(收入![]() 支出),求该店员工人数;
支出),求该店员工人数;
![]() 若该店只有
若该店只有![]() 名员工,则该店至少需要多少天才能还清贷款,此时,每件服装的价格应定为多少元?
名员工,则该店至少需要多少天才能还清贷款,此时,每件服装的价格应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com