
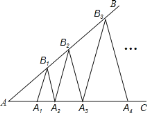
【题目】 已知∠BAC=36°,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是顶角为36°的等腰三角形,即∠A1B1A2=∠A2B2A3=∠A3B3A4=…=∠AnBnAn+1=36°,点A1,A2,A3,…,An在射线AC上,点B1,B2,B3,…,Bn在射线AB上,若A1A2=1,则线段A2018A2019的长为______.
【答案】
【解析】
先证明△A2B1A1∽△A2AB1,设AA1=A1B1=B1A2=x,则有![]() =
=![]() ,从而可求出x的值,同理可得A2A3的长,A3A4的长,…,根据规律可得出结果.
,从而可求出x的值,同理可得A2A3的长,A3A4的长,…,根据规律可得出结果.
解:∵∠A=∠A1B1A2=36°,A1B1=A2B1,
∴∠AA2B1=∠B1A1A2=72°,
∴∠A=∠AB1A1=36°,
∴AA1=A1B1=B1A2,△A2B1A1∽△A2AB1,
设AA1=A1B1=B1A2=x,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得x=![]() (舍去负根),
(舍去负根),
同理可得:AA2=A2B2=B2A3=1+![]() ,
,
设A2A3=y,
∵△A3B2A2∽△A3AB2,
∴![]() =
=![]() ,
,
∴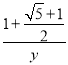 =
=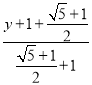 ,
,
解得:y=![]() ,即A2A3=
,即A2A3=![]() ,
,
同理可得:A3A4=(![]() )2,…
)2,…
∴A2018A2019的长=(![]() )2017,
)2017,
故答案为: .
.


科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,经市场调查发现:该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如表:
售价x(元/件) | 30 | 40 | 60 |
周销售量y(件) | 90 | 70 | 30 |
周销售利润w(元) | 450 | 1050 | 1050 |
注:周销售利润=周销售量×(售价﹣进价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)当售价定为多少时,周销售利润最大,最大利润是多少?
(3)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过45元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1080元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
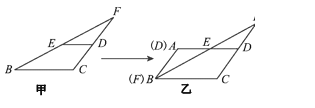
【题目】如图甲,已知ED是△FBC的中位线,沿线段ED将△FED剪下后拼接在图乙中△BEA的位置.
(1)从△FED到△BEA的图形变换,可以认为是(填平移或轴对称或旋转)变换;
(2)试判断图乙中四边形ABCD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的不等式组 有且只有四个整数解,又关于x的分式方程
有且只有四个整数解,又关于x的分式方程![]() ﹣2=
﹣2=![]() 有正数解,则满足条件的整数k的和为( )
有正数解,则满足条件的整数k的和为( )
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料
计算:(1﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() )﹣(1﹣
)﹣(1﹣![]() ﹣
﹣![]() )(
)(![]() +
+![]() ),令
),令![]() +
+![]() =t,则:
=t,则:
原式=(1﹣t)(t+![]() )﹣(1﹣t﹣
)﹣(1﹣t﹣![]() )t=t+
)t=t+![]() ﹣t2﹣
﹣t2﹣![]() +t2=
+t2=![]()
在上面的问题中,用一个字母代表式子中的某一部分,能达到简化计算的目的,这种思想方法叫做“换元法”,请用“换元法”解决下列问题:
(1)计算:(1﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() )﹣(1﹣
)﹣(1﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() )
)
(2)因式分解:(a2﹣5a+3)(a2﹣5a+7)+4
(3)解方程:(x2+4x+1)(x2+4x+3)=3
查看答案和解析>>
科目:初中数学 来源: 题型:
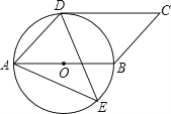
【题目】 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O半径为4cm,AE=6cm,求∠ADE的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD是矩形,过点D作DF∥AC交BA的延长线于点F.
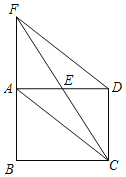
(1)求证:四边形ACDF是平行四边形;
(2)若AB=3,DF=5,求△AEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+c(a<0)经过点A、B.
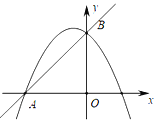
(1)求a、b满足的关系式及c的值.
(2)当x<0时,若y=ax2+bx+c(a<0)的函数值随x的增大而增大,求a的取值范围.
(3)如图,当a=﹣1时,在抛物线上是否存在点P,使△PAB的面积为1?若存在,请求出符合条件的所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com