
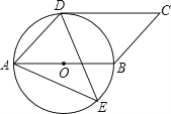
【题目】 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O半径为4cm,AE=6cm,求∠ADE的正切值.
【答案】(1)CD与⊙O相切,理由见解析;(2)![]()
【解析】
(1)连接OD,首先根据圆周角定理求出∠AOD=90°,然后利用平行四边形的性质得到AB∥DC,利用平行线的性质即可得出结论;
(2)连接BE,则∠ADE=∠ABE,由AB是⊙O的直径得到∠AEB=90°,而AB=2×4=8(cm).在Rt△ABE中,根据勾股定理求出BE的长,再利用三角函数的定义即可求解.
解:(1)CD与⊙O相切.
理由如下:连接OD.
则∠AOD=2∠AED=2×45°=90°,
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠CDO=∠AOD=90°.
∴OD⊥CD,
∴CD与⊙O相切;
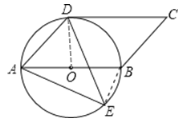
(2)连接BE,则∠ADE=∠ABE.
∵AB是⊙O的直径,
∴∠AEB=90°,AB=2×4=8(cm).
在Rt△ABE中,
由勾股定理得,BE=![]() (cm),
(cm),
∴tan∠ABE=![]() .
.
∴∠ADE的正切值为![]() .
.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】已知:在△ABC 中,AB=AC.
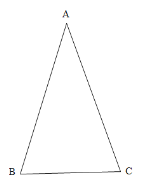
(1)求作△ABC 外接圆(尺规作图)
(2)若△ABC 的外接圆的圆心O到 BC 边的距离为 4,BC=6,求外接圆的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC.
(操作)(1)将△ABD绕点D沿顺时针方向旋转60°,在图中画出旋转后的三角形.
(探究)(2)结合所画图形探究BD与AB,BC之间的数量关系,并证明你的结论.
(应用)(3)若AB=6,BC=8,试求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
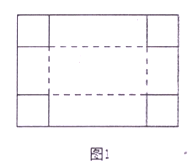
【题目】数学综合实践课上,老师提出问题:如图,有一张长为![]() ,宽为
,宽为![]() 的长方形纸板,在纸板四个角剪去四个相同的小正方形,然后把四边折起来(实线为剪裁线,虚线为折叠线),做成一个无盖的长方体盒子,问小正方形的边长为多少时,盒子的体积最大?为了解决这个问题,小明同学根据学习函数的经验,进行了如下的探究:
的长方形纸板,在纸板四个角剪去四个相同的小正方形,然后把四边折起来(实线为剪裁线,虚线为折叠线),做成一个无盖的长方体盒子,问小正方形的边长为多少时,盒子的体积最大?为了解决这个问题,小明同学根据学习函数的经验,进行了如下的探究:
(1)设小正方形的边长为![]() ,长方体体积为
,长方体体积为![]() ,根据长方体的体积公式,可以得到
,根据长方体的体积公式,可以得到![]() 与
与![]() 的函数关系式是 ,其中自变量
的函数关系式是 ,其中自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)列出![]() 与
与![]() 的几组对应值如下表:
的几组对应值如下表:
| … |
|
|
|
|
|
|
| 1 |
|
| … |
| … | 1.3 | 2.2 | 2.7 | 3.0 | 2.8 | 2.5 | 1.5 | 0.9 | … |
(注:补全表格,保留1位小数点)
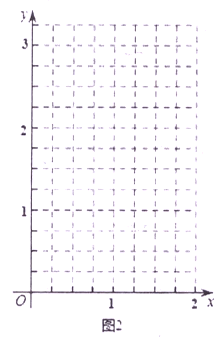
(3)如图,请在平面直角坐标系中描出以补全后表格中各对对应值为坐标的点,画出该函数图象;
(4)结合函数图象回答:当小正方形的边长约为 ![]() 时,无盖长方体盒子的体积最大,最
时,无盖长方体盒子的体积最大,最
大值约为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知∠BAC=36°,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是顶角为36°的等腰三角形,即∠A1B1A2=∠A2B2A3=∠A3B3A4=…=∠AnBnAn+1=36°,点A1,A2,A3,…,An在射线AC上,点B1,B2,B3,…,Bn在射线AB上,若A1A2=1,则线段A2018A2019的长为______.
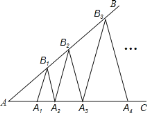
查看答案和解析>>
科目:初中数学 来源: 题型:
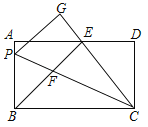
【题目】如图,在矩形ABCD中,AB=12,P是AB上一点,将△PBC沿直线PC折叠,顶点B的对应点是G,过点B作BE⊥CG,垂足为E,且在AD上,BE交PC于点F,则下列结论,其中正确的结论有( )
①BP=BF;②若点E是AD的中点,那么△AEB≌△DEC;③当AD=25,且AE<DE时,则DE=16;④在③的条件下,可得sin∠PCB=![]() ;⑤当BP=9时,BEEF=108.
;⑤当BP=9时,BEEF=108.
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
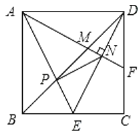
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则以下结论中:①F为CD的中点;②3AM=2DE;③tan∠EAF=![]() ;④
;④![]() ;⑤△PMN∽△DPE,正确的结论个数是( )
;⑤△PMN∽△DPE,正确的结论个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
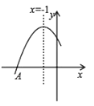
【题目】如图是二次函数![]() 图像的一部分,图像过点 A(-3,0)顶点坐标为(-1,n)给出以下结论(1)abc<0;(2)b2-4ac>0 ;(3)当
图像的一部分,图像过点 A(-3,0)顶点坐标为(-1,n)给出以下结论(1)abc<0;(2)b2-4ac>0 ;(3)当![]() 时,
时,![]() ;(4)若 B(-
;(4)若 B(- ![]() ,y1 ), C (-
,y1 ), C (-![]() , y2)为函数图像上的两点,则
, y2)为函数图像上的两点,则![]() ;(5)方程
;(5)方程![]() 有两个不相等的实数根.其中正确的有( )
有两个不相等的实数根.其中正确的有( )
A.2 个B.3 个C.4 个D.5 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com