
【题目】已知:在△ABC 中,AB=AC.
(1)求作△ABC 外接圆(尺规作图)
(2)若△ABC 的外接圆的圆心O到 BC 边的距离为 4,BC=6,求外接圆的面积.
【答案】(1)图见解析;(2)![]() .
.
【解析】
(1)分别作BC边和AC边的垂直平分线,两者的交点即为外接圆的圆心O,再连接OB,以点O为圆心,OB为半径画圆即可;
(2)根据垂径定理,图中(见解析)点D为BC边的中点,OD为圆心O到BC边的距离,在![]() 中可求得半径OB的长,再利用圆的面积公式即可得.
中可求得半径OB的长,再利用圆的面积公式即可得.
(1)因为三角形外接圆的圆心是三角形三条边的垂直平分线的交点,所以画出三条边的垂直平分线的交点O,再连接OB,以点O为圆心,OB为半径画圆就是所要画的外接圆,又因为三条边的垂直平分线必交于一点,所以只要画出两边的垂直平分线的交点即可,以BC边的垂直平分线画法为例:分别以B、C两点为圆心,以大于BC边的二分之一为半径画弧线,得到两个交点,连接这两个交点就可得到BC的垂直平分线 同样地方法,画出AC边的垂直平分线,两条垂直平分线的交点为点O,画图结果如下:
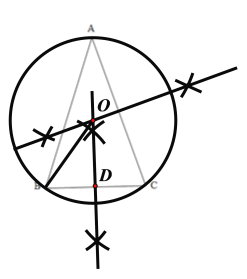
(2)由垂径定理得,题(1)的图中,点D为BC的中点,且![]()
则![]() ,
,
由勾股定理得:半径![]() ,
,
故外接圆的面积![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
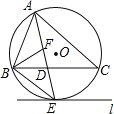
【题目】如图,圆O是![]() 的外接圆,AE平分
的外接圆,AE平分![]() 交圆O于点E,交BC于点D,过点E作直线
交圆O于点E,交BC于点D,过点E作直线![]() .
.
(1)判断直线l与圆O的关系,并说明理由;
(2)若![]() 的平分线BF交AD于点F,求证:
的平分线BF交AD于点F,求证:![]() ;
;
(3)在(2)的条件下,若![]() ,
,![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2019年的到来,铜陵万达广场某商铺将进价为40元的礼盒按50元售出时,能卖出500盒.商铺发现这种礼盒每涨价0.1元时,其销量就减少1盒.
(1)若该商铺计划赚得9000元的利润,售价应定为多少元?
(2)物价部门规定:该礼盒售价不得超过进价的1.5倍.问:此时礼盒售价定为多少元,才能使得商铺的获利最大?且最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
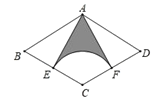
【题目】如图,在菱形ABCD中,点E是BC的中点,以C为圆心、CE为半径作弧,交CD于点F,连接AE、AF.若AB=2,∠B=60°,则阴影部分的面积为( )
A.![]()
![]() B.
B.![]()
![]()
C.2![]() –πD.2
–πD.2![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,经市场调查发现:该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如表:
售价x(元/件) | 30 | 40 | 60 |
周销售量y(件) | 90 | 70 | 30 |
周销售利润w(元) | 450 | 1050 | 1050 |
注:周销售利润=周销售量×(售价﹣进价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)当售价定为多少时,周销售利润最大,最大利润是多少?
(3)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过45元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1080元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
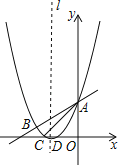
【题目】如图,抛物线y=![]() x2+bx+c与直线y=
x2+bx+c与直线y=![]() x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).
x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).
(1)求抛物线的解析式;
(2)在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;
(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商投产一种新型电子产品,每件制造成本为16元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)如果厂商每月的制造成本不超过480万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=4,矩形DEFG的顶点D、G分别在AC、BC上,边EF在AB上.
(1)求证:△AED∽△DCG;
(2)若矩形DEFG的面积为4,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
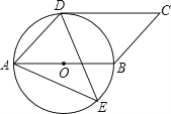
【题目】 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O半径为4cm,AE=6cm,求∠ADE的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com