
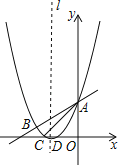
【题目】如图,抛物线y=![]() x2+bx+c与直线y=
x2+bx+c与直线y=![]() x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).
x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).
(1)求抛物线的解析式;
(2)在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;
(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式是y=![]() x2+
x2+![]() x+3;(2)|MB﹣MD|取最大值为
x+3;(2)|MB﹣MD|取最大值为![]() ;(3)存在点P(1,6).
;(3)存在点P(1,6).
【解析】(1)根据待定系数法,可得函数解析式;
(2)根据对称性,可得MC=MD,根据解方程组,可得B点坐标,根据两边之差小于第三边,可得B,C,M共线,根据勾股定理,可得答案;
(3)根据等腰直角三角形的判定,可得∠BCE,∠ACO,根据相似三角形的判定与性质,可得关于x的方程,根据解方程,可得x,根据自变量与函数值的对应关系,可得答案.
(1)将A(0,3),C(﹣3,0)代入函数解析式,得
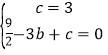 ,解得
,解得![]() ,
,
抛物线的解析式是y=![]() x2+
x2+![]() x+3;
x+3;
(2)由抛物线的对称性可知,点D与点C关于对称轴对称,
∴对l上任意一点有MD=MC,
联立方程组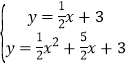 ,
,
解得![]() (不符合题意,舍),
(不符合题意,舍),![]() ,
,
∴B(﹣4,1),
当点B,C,M共线时,|MB﹣MD|取最大值,即为BC的长,
过点B作BE⊥x轴于点E,
 ,
,
在Rt△BEC中,由勾股定理,得
BC=![]() ,
,
|MB﹣MD|取最大值为![]() ;
;
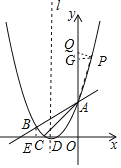
(3)存在点P使得以A,P,Q为顶点的三角形与△ABC相似,
在Rt△BEC中,∵BE=CE=1,
∴∠BCE=45°,
在Rt△ACO中,
∵AO=CO=3,
∴∠ACO=45°,
∴∠ACB=180°﹣45°﹣45°=90°,
过点P作PQ⊥y轴于Q点,∠PQA=90°,
设P点坐标为(x,![]() x2+
x2+![]() x+3)(x>0)
x+3)(x>0)
①当∠PAQ=∠BAC时,△PAQ∽△CAB,
∵∠PGA=∠ACB=90°,∠PAQ=∠CAB,
∴△PGA∽△BCA,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
解得x1=1,x2=0(舍去),
∴P点的纵坐标为![]() ×12+
×12+![]() ×1+3=6,
×1+3=6,
∴P(1,6),
②当∠PAQ=∠ABC时,△PAQ∽△CBA,
∵∠PGA=∠ACB=90°,∠PAQ=∠ABC,
∴△PGA∽△ACB,
∴![]() ,
,
即![]() =3,
=3,
∴![]() ,
,
解得x1=﹣![]() (舍去),x2=0(舍去)
(舍去),x2=0(舍去)
∴此时无符合条件的点P,
综上所述,存在点P(1,6).


科目:初中数学 来源: 题型:
【题目】为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放![]() 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校科技小组进行野外考察,途中遇到一片湿地,为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道,木板对地面的压强![]() 是木板面积
是木板面积![]() 的反比例函数,其图像如下图所示:
的反比例函数,其图像如下图所示:
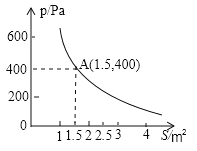
(1)请直接写出这一函数表达式和自变量取值范围;
(2)当木板面积为![]() 时,压强是多少?
时,压强是多少?
(3)如果要求压强不超过![]() ,木板的面积至少要多大?
,木板的面积至少要多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小马、小虎两人共同计算一道题:(x+a)(2x+b).由于小马抄错了a的符号,得到的结果是2x2﹣7x+3,小虎漏抄了第二个多项式中x的系数得到的结果是x2+2x﹣3.
(1)求a,b的值;
(2)细心的你请计算这道题的正确结果;
(3)当x=﹣1时,计算(2)中的代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
①经过三个点一定可以作圆;②若等腰三角形的两边长分别为3和7,则第三边长是3或7;③一个正六边形的内角和是其外角和的2倍;④随意翻到一本书的某页,页码是偶数是随机事件;⑤关于x的一元二次方程x2-(k+3)x+k=0有两个不相等的实数根.
A.①②③B.①④⑤C.②③④D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣2,0),等边△AOC经过平移或轴对称或旋转都可以得到△OBD.
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个单位长度;△AOC与△BOD关于直线对称,则对称轴是 ;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是 度.
(2)连接AD,交OC于点E,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:

①旋转角的度数;
②线段OD的长;
③∠BDC的度数.
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA、OB、OC满足什么条件时,∠ODC=90°?请给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程tx26x+m+4=0有两个实数根x1、x2.
(1)当m=1时,求t的取值范围;
(2)当t=1时,若x1、x2满足3| x1|=x2+4,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在《九章算术》“勾股”章中有这样一个问题:
“今有邑方不知大小,各中开门,出北门二十步有木,出南门十回步,折而西行一千七百七十五步见木.问邑方几何.”用今天的话说,大意是:如图,DEFG是一座正方形小城,北门H位于DG的中点,南门K位于EF的中点,出北门20步到A处有一树木,出南门14步到C,再向西行1775步到B处,正好看到A处的树木(即点D在直线AB上),求小城的边长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com