练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在《九章算术》“勾股”章中有这样一个问题:

    “今有邑方不知大小，各中开门，出北门二十步有木，出南门十回步，折而西行一千七百七十五步见木.问邑方几何.”用今天的话说，大意是:如图，DEFG是一座正方形小城，北门H位于DG的中点，南门K位于EF的中点，出北门20步到A处有一树木，出南门14步到C，再向西行1775步到B处，正好看到A处的树木(即点D在直线AB上)，求小城的边长.

    【答案】小城的边长为250步.

    【解析】

    设小城的边长为x步，利用Rt△AHD∽Rt△ACB可得比例关系，代入相关数据即可计算.

    设小城的边长为x步，根据题意，Rt△AHD∽Rt△ACB，

    因为有，即，去分母并整理，得x2+34x-71000=0，

    解得x1=250，x2=-284(不合题意，舍去)，

    故小城的边长为250步.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

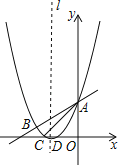
    【题目】如图，抛物线y=x2+bx+c与直线y=x+3交于A，B两点，交x轴于C、D两点，连接AC、BC，已知A（0，3），C（﹣3，0）．

    （1）求抛物线的解析式；

    （2）在抛物线对称轴l上找一点M，使|MB﹣MD|的值最大，并求出这个最大值；

    （3）点P为y轴右侧抛物线上一动点，连接PA，过点P作PQ⊥PA交y轴于点Q，问：是否存在点P使得以A，P，Q为顶点的三角形与△ABC相似？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，有一个长为米的篱笆，一面利用墙（墙的最大长度为米）围成的中间隔有一道篱笆的长方形花圃．设花圃的宽为米，面积为平方米．

    求与的函数关系式；

    如果要围成花圃的面积为平方米，求的长为多少米？

    如果要使围成花圃面积最大，求的长为多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】当取何值时，下列各式在实数范围内有意义？

    （1）；

    （2）；

    （3）；

    （4）；

    （5）；

    （6）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线l1：y=2x+1与坐标轴交于A、C两点，直线l2：y=﹣x﹣2与坐标轴交于B、D两点，两线的交点为P点，

    （1）求出点P的坐标；

    （2）求△APB的面积；

    （3）在x轴上是否存在点Q,使得△OPQ的面积等于6，若存在，求出Q点坐标，若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

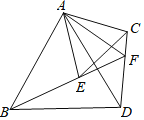
    【题目】如图，，分别以AB、AC为边作等边三角形ABD与等边三角形ACE，连接BE、CD，BE的延长线与CD交于点F，连接AF，有以下四个结论：①；②FA平分；③；④．其中一定正确的结论有（ ）

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面的网格中，每个小正方形的边长均为1个单位．小正方形的顶点叫做格点，以О点为原点，以过О点的水平直线MN为x轴建立平面直角坐标系．

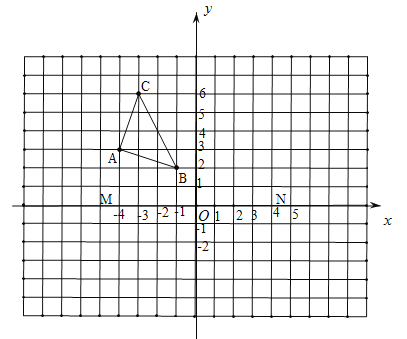
    （1）与格点是关于y轴对称，画出；

    （2）格点Р在第二象限内，且为等腰直角（注：P不在的边上），画出，并直接写出Р点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为了鼓励居民节约用水，决定实行两级收费制度，若每月用水量不超过14吨（含14吨），则每吨按政府补贴优惠价m元收费；若每月用水量超过14吨，则超过部分每吨按市场价n元收费．小明家3月份用水20吨，交水费49元；4月份用水18吨，交水费42元．

    （1）求每吨水的政府补贴优惠价m和市场价n分别是多少元？

    （2）小明家5月份交水费70元，则5月份他家用了多少吨水？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知反比例函数的图像与一正比例函数的图像相交于点，点的坐标是.

    （1）求正比例函数的解析式；

    （2）若正比例函数的图像与反比例函数的图像在第一象限内交于点，过点作轴的垂线，为垂足，且交直线于点，过点作轴的垂线，为垂足，求梯形的面积；

    （3）连结，求的面积.

    查看答案和解析>>

    同步练习册答案