
【题目】如图,有一个长为![]() 米的篱笆,一面利用墙(墙的最大长度
米的篱笆,一面利用墙(墙的最大长度![]() 为
为![]() 米)围成的中间隔有一道篱笆的长方形花圃.设花圃的宽
米)围成的中间隔有一道篱笆的长方形花圃.设花圃的宽![]() 为
为![]() 米,面积为
米,面积为![]() 平方米.
平方米.

![]() 求
求![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 如果要围成花圃的面积为
如果要围成花圃的面积为![]() 平方米,求
平方米,求![]() 的长为多少米?
的长为多少米?
![]() 如果要使围成花圃面积最大,求
如果要使围成花圃面积最大,求![]() 的长为多少米?
的长为多少米?
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】某校科技小组进行野外考察,途中遇到一片湿地,为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道,木板对地面的压强![]() 是木板面积
是木板面积![]() 的反比例函数,其图像如下图所示:
的反比例函数,其图像如下图所示:
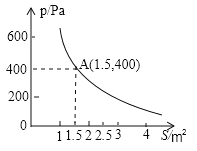
(1)请直接写出这一函数表达式和自变量取值范围;
(2)当木板面积为![]() 时,压强是多少?
时,压强是多少?
(3)如果要求压强不超过![]() ,木板的面积至少要多大?
,木板的面积至少要多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:

①旋转角的度数;
②线段OD的长;
③∠BDC的度数.
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA、OB、OC满足什么条件时,∠ODC=90°?请给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程tx26x+m+4=0有两个实数根x1、x2.
(1)当m=1时,求t的取值范围;
(2)当t=1时,若x1、x2满足3| x1|=x2+4,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强课外阅读,开阔视野,我校开展了“书香校园”的主题活动.学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制成如下频数分布表和不完整的频数直方
图:


请根据图表信息回答下列问题:
(1)频数分布表中的a=_______,b=_______;
(2)将频数直方图补充完整;
(3)全校共有学生1200人,若规定阅读时间超过2小时则评为“优秀阅读员”,请估计能评为“优秀阅读员”的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在《九章算术》“勾股”章中有这样一个问题:
“今有邑方不知大小,各中开门,出北门二十步有木,出南门十回步,折而西行一千七百七十五步见木.问邑方几何.”用今天的话说,大意是:如图,DEFG是一座正方形小城,北门H位于DG的中点,南门K位于EF的中点,出北门20步到A处有一树木,出南门14步到C,再向西行1775步到B处,正好看到A处的树木(即点D在直线AB上),求小城的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-2(k+1)x+k2+2k=0.
(1)求证:k取任何实数值,方程总有不相等的实数根;
(2)若等腰△ABC的周长为14,另两边长b,c恰好是这个方程的两个根,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com