
【题目】已知关于x的方程x2-2(k+1)x+k2+2k=0.
(1)求证:k取任何实数值,方程总有不相等的实数根;
(2)若等腰△ABC的周长为14,另两边长b,c恰好是这个方程的两个根,求k的值.
【答案】(1)证明见解析;(2)k=4 或![]() .
.
【解析】
(1)、根据题意得出a、b、c的值,然后求出△=b2-4ac的值,从而得出方程的解的个数;(2)、首先根据方程的解法求出x1=k,x2=k+1,设b=k,c=k+2,根据等腰三角形的性质进行分类讨论,从而得出k的值.
(1)、证明: ∵a=1,b=-2(k+1),c=k2+2k,∴△=b2-4ac=[-2(k+1)]2-4(k2+2k)=4>0,
∴方程有两个不相等的实数根;
(2)、解:原方程x2-2(k+1)x+k2+2k=0.解得:x1=k,x2=k+1,
∵b,c恰好是方程的两个根,∴设b=k,c=k+2, ∵方程有两个不相等的实数根;∴b≠c,
①、当b为腰时,则2b+c=14,∵c-b=2, ∴b=4,c=6, 即k=4
②、当c为腰时,则2c+b=14,∵c-b=2, ∴b=![]() ,c=
,c=![]() , 即k=
, 即k=![]()
综上所述:k=4 或![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,有一个长为![]() 米的篱笆,一面利用墙(墙的最大长度
米的篱笆,一面利用墙(墙的最大长度![]() 为
为![]() 米)围成的中间隔有一道篱笆的长方形花圃.设花圃的宽
米)围成的中间隔有一道篱笆的长方形花圃.设花圃的宽![]() 为
为![]() 米,面积为
米,面积为![]() 平方米.
平方米.

![]() 求
求![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 如果要围成花圃的面积为
如果要围成花圃的面积为![]() 平方米,求
平方米,求![]() 的长为多少米?
的长为多少米?
![]() 如果要使围成花圃面积最大,求
如果要使围成花圃面积最大,求![]() 的长为多少米?
的长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的网格中,每个小正方形的边长均为1个单位.小正方形的顶点叫做格点,以О点为原点,以过О点的水平直线MN为x轴建立平面直角坐标系.
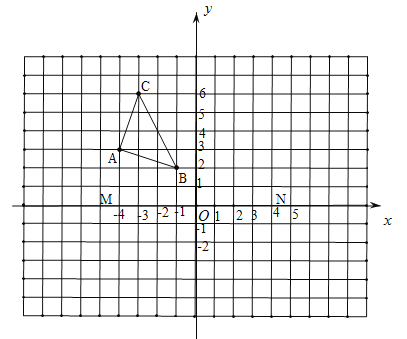
(1)![]() 与格点
与格点![]() 是关于y轴对称,画出
是关于y轴对称,画出![]() ;
;
(2)格点Р在第二象限内,且![]() 为等腰直角
为等腰直角![]() (注:P不在
(注:P不在![]() 的边上),画出
的边上),画出![]() ,并直接写出Р点坐标.
,并直接写出Р点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度,若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价m和市场价n分别是多少元?
(2)小明家5月份交水费70元,则5月份他家用了多少吨水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA
与⊙O的另一个交点为E,连结AC,CE。

(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
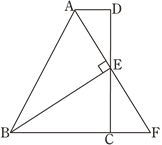
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F. 已知AD=2cm,BC=5cm.
(1)求证:FC=AD;
(2)求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一抛物线形大门,其地面宽度![]() .一同学站在门内,在离门脚
.一同学站在门内,在离门脚![]() 点
点![]() 远的
远的![]() 处,垂直地面立
处,垂直地面立
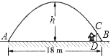
起一根![]() 长的木杆,其顶端恰好顶在抛物线形门上
长的木杆,其顶端恰好顶在抛物线形门上![]() 处.根据这些条件,请你求出该大门的高
处.根据这些条件,请你求出该大门的高![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图像与一正比例函数的图像相交于点
的图像与一正比例函数的图像相交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
(1)求正比例函数的解析式;
(2)若正比例函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像在第一象限内交于点
的图像在第一象限内交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,
轴的垂线,![]() 为垂足,且交直线
为垂足,且交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,
轴的垂线,![]() 为垂足,求梯形
为垂足,求梯形![]() 的面积;
的面积;
(3)连结![]() ,求
,求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+2的图象经过点A,且y随x的增大而减小.则A点的坐标可以是( )
A.(2,5)B.(﹣1,1)C.(3,0)D.(![]() ,4)
,4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com