
【题目】如图,已知反比例函数![]() 的图像与一正比例函数的图像相交于点
的图像与一正比例函数的图像相交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
(1)求正比例函数的解析式;
(2)若正比例函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像在第一象限内交于点
的图像在第一象限内交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,
轴的垂线,![]() 为垂足,且交直线
为垂足,且交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,
轴的垂线,![]() 为垂足,求梯形
为垂足,求梯形![]() 的面积;
的面积;
(3)连结![]() ,求
,求![]() 的面积.
的面积.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在《九章算术》“勾股”章中有这样一个问题:
“今有邑方不知大小,各中开门,出北门二十步有木,出南门十回步,折而西行一千七百七十五步见木.问邑方几何.”用今天的话说,大意是:如图,DEFG是一座正方形小城,北门H位于DG的中点,南门K位于EF的中点,出北门20步到A处有一树木,出南门14步到C,再向西行1775步到B处,正好看到A处的树木(即点D在直线AB上),求小城的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-2(k+1)x+k2+2k=0.
(1)求证:k取任何实数值,方程总有不相等的实数根;
(2)若等腰△ABC的周长为14,另两边长b,c恰好是这个方程的两个根,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仙降是瑞安重要的制鞋基地,其生产的鞋子畅销世界各地,某制鞋企业欲将![]() 件产品运往
件产品运往![]() 三地销售,运往
三地销售,运往![]() 地的费用为18元/件,运往
地的费用为18元/件,运往![]() 地的费用为20元/件,运往
地的费用为20元/件,运往![]() 地的费用为17元/件,要求运往
地的费用为17元/件,要求运往![]() 地的件数与运往
地的件数与运往![]() 地的件数相同. 设安排
地的件数相同. 设安排![]() 件产品运往
件产品运往![]() 地.
地.
(1)若![]() ①运往
①运往![]() 地件数为 件(用含
地件数为 件(用含![]() 的代数式表示);②若总运费不超过1850元,则运往
的代数式表示);②若总运费不超过1850元,则运往![]() 地至少有多少件?
地至少有多少件?
(2)若总运费为1900元,则![]() 的最大值为 .(直接写出答案)
的最大值为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
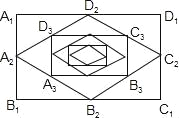
【题目】如图:顺次连接矩形A1B1C1D1四边的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得四边形A3B3C3D3,…,按此规律得到四边形AnBnCnDn.若矩形A1B1C1D1的面积为24,那么四边形A2019B2019C2019D2019的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,经过C作CD⊥AB于点D,CF是⊙O的切线,过点A作AE⊥CF于E,连接AC.
(1)求证:AE=AD.
(2)若AE=3,CD=4,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,点E是CD上一点,AE平分∠BAD,BF平分∠ABC,延长BE交AD的延长线于点F
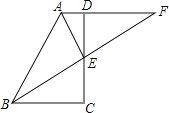
(1)求证:△ABE≌△AFE;
(2)若AD=2,BC=6,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 与x、y轴分别交于A、B两点,
与x、y轴分别交于A、B两点,![]() 与x、y轴交于C、D两点.
与x、y轴交于C、D两点.
(1)求A、B、C、D的坐标(用含k、m的代数式表示);
(2)若![]() ,求
,求![]() 的值;
的值;
(3)在(2)的前提下,若![]() 的面积为27,求m的值.
的面积为27,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com