
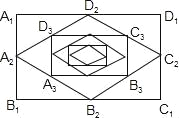
【题目】如图:顺次连接矩形A1B1C1D1四边的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得四边形A3B3C3D3,…,按此规律得到四边形AnBnCnDn.若矩形A1B1C1D1的面积为24,那么四边形A2019B2019C2019D2019的面积为_____.
【答案】![]()
【解析】
根据已知条件可得四边形A2B2C2D2的面积=![]() 矩形A1B1C1D1的面积;四边形A3B3C3D3=
矩形A1B1C1D1的面积;四边形A3B3C3D3=![]() 四边形A2B2C2D2的面积=
四边形A2B2C2D2的面积=![]() 矩形A1B1C1D1的面积;由此可得四边形AnBnCnDn的面积=
矩形A1B1C1D1的面积;由此可得四边形AnBnCnDn的面积=![]() 矩形A1B1C1D1的面积.根据所得规律求解即可.
矩形A1B1C1D1的面积.根据所得规律求解即可.
∵四边形A1B1C1D1是矩形,
∴∠A1=∠B1=∠C1=∠D1=90°,A1B1=C1D1,B1C1=A1D1;
又∵各边中点是A2、B2、C2、D2,
∴四边形A2B2C2D2的面积=S△A1A2D2+S△C2D1D2+S△C1B2C2+S△B1B2A2
=![]()
![]() A1D1
A1D1![]() A1B1×4=
A1B1×4=![]() 矩形A1B1C1D1的面积,
矩形A1B1C1D1的面积,
即四边形A2B2C2D2的面积=![]() 矩形A1B1C1D1的面积;
矩形A1B1C1D1的面积;
同理,得四边形A3B3C3D3=![]() 四边形A2B2C2D2的面积=
四边形A2B2C2D2的面积=![]() 矩形A1B1C1D1的面积;
矩形A1B1C1D1的面积;
以此类推,四边形AnBnCnDn的面积=![]() 矩形A1B1C1D1的面积.
矩形A1B1C1D1的面积.
又∵矩形A1B1C1D1的面积为24,
∴四边形A2019B2019C2019D2019的面积为![]() .
.
故答案是:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知直线l1:y=2x+1与坐标轴交于A、C两点,直线l2:y=﹣x﹣2与坐标轴交于B、D两点,两线的交点为P点,
(1)求出点P的坐标;
(2)求△APB的面积;
(3)在x轴上是否存在点Q,使得△OPQ的面积等于6,若存在,求出Q点坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA
与⊙O的另一个交点为E,连结AC,CE。

(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一抛物线形大门,其地面宽度![]() .一同学站在门内,在离门脚
.一同学站在门内,在离门脚![]() 点
点![]() 远的
远的![]() 处,垂直地面立
处,垂直地面立
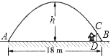
起一根![]() 长的木杆,其顶端恰好顶在抛物线形门上
长的木杆,其顶端恰好顶在抛物线形门上![]() 处.根据这些条件,请你求出该大门的高
处.根据这些条件,请你求出该大门的高![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图像与一正比例函数的图像相交于点
的图像与一正比例函数的图像相交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
(1)求正比例函数的解析式;
(2)若正比例函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像在第一象限内交于点
的图像在第一象限内交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,
轴的垂线,![]() 为垂足,且交直线
为垂足,且交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,
轴的垂线,![]() 为垂足,求梯形
为垂足,求梯形![]() 的面积;
的面积;
(3)连结![]() ,求
,求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD的边长是4,∠ABC=120°,点M、N分别在边AD、AB上,且MN⊥AC,垂足为P,把△AMN沿MN折叠得到△AˊMN,若△AˊDC恰为等腰三角形,则AP的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息有:①甲队挖掘30m时,用了3h;②挖掘6h时甲队比乙队多挖了10m;③乙队的挖掘速度总是小于甲队;④开挖后甲、乙两队所挖河渠长度相等时,x=4.其中一定正确的有( )
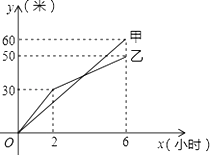
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是三边都不相等的三角形,点O和点P是这个三角形内部两点.
(1)如图①,如果点P是这个三角形三个内角平分线的交点,那么∠BPC和∠BAC有怎样的数量关系?请说明理由;
(2)如图②,如果点O是这个三角形三边垂直平分线的交点,那么∠BOC和∠BAC有怎样的数量关系?请说明理由;
(3)如图③,如果点P(三角形三个内角平分线的交点),点O(三角形三边垂直平分线的交点)同时在不等边△ABC的内部,那么∠BPC和∠BOC有怎样的数量关系?请直接回答.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com