
【题目】如图,已知一抛物线形大门,其地面宽度![]() .一同学站在门内,在离门脚
.一同学站在门内,在离门脚![]() 点
点![]() 远的
远的![]() 处,垂直地面立
处,垂直地面立
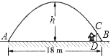
起一根![]() 长的木杆,其顶端恰好顶在抛物线形门上
长的木杆,其顶端恰好顶在抛物线形门上![]() 处.根据这些条件,请你求出该大门的高
处.根据这些条件,请你求出该大门的高![]() .
.
科目:初中数学 来源: 题型:
【题目】为了加强课外阅读,开阔视野,我校开展了“书香校园”的主题活动.学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制成如下频数分布表和不完整的频数直方
图:


请根据图表信息回答下列问题:
(1)频数分布表中的a=_______,b=_______;
(2)将频数直方图补充完整;
(3)全校共有学生1200人,若规定阅读时间超过2小时则评为“优秀阅读员”,请估计能评为“优秀阅读员”的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙ P的圆心坐标是(2,a)(a>2),半径为2,函数y=x的图象被⊙ P截得的弦AB的长为![]() ,则a的值是 ( )
,则a的值是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-2(k+1)x+k2+2k=0.
(1)求证:k取任何实数值,方程总有不相等的实数根;
(2)若等腰△ABC的周长为14,另两边长b,c恰好是这个方程的两个根,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:AE⊥AB,AF⊥AC,AE=AB,AF=AC,
(1)图中EC、BF有怎样的数量和位置关系?试证明你的结论.
(2)连接AM,求证:MA平分∠EMF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仙降是瑞安重要的制鞋基地,其生产的鞋子畅销世界各地,某制鞋企业欲将![]() 件产品运往
件产品运往![]() 三地销售,运往
三地销售,运往![]() 地的费用为18元/件,运往
地的费用为18元/件,运往![]() 地的费用为20元/件,运往
地的费用为20元/件,运往![]() 地的费用为17元/件,要求运往
地的费用为17元/件,要求运往![]() 地的件数与运往
地的件数与运往![]() 地的件数相同. 设安排
地的件数相同. 设安排![]() 件产品运往
件产品运往![]() 地.
地.
(1)若![]() ①运往
①运往![]() 地件数为 件(用含
地件数为 件(用含![]() 的代数式表示);②若总运费不超过1850元,则运往
的代数式表示);②若总运费不超过1850元,则运往![]() 地至少有多少件?
地至少有多少件?
(2)若总运费为1900元,则![]() 的最大值为 .(直接写出答案)
的最大值为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
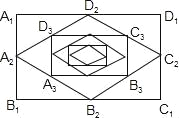
【题目】如图:顺次连接矩形A1B1C1D1四边的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得四边形A3B3C3D3,…,按此规律得到四边形AnBnCnDn.若矩形A1B1C1D1的面积为24,那么四边形A2019B2019C2019D2019的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,经过C作CD⊥AB于点D,CF是⊙O的切线,过点A作AE⊥CF于E,连接AC.
(1)求证:AE=AD.
(2)若AE=3,CD=4,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,点
,点![]() 在该函数的图象上,点
在该函数的图象上,点![]() 到
到![]() 轴、
轴、![]() 轴的距离分别为
轴的距离分别为![]() 、
、![]() .设
.设![]() ,下列结论中:
,下列结论中:
①![]() 没有最大值;②
没有最大值;②![]() 没有最小值;③
没有最小值;③![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
④满足![]() 的点
的点![]() 有四个.其中正确结论的个数有( )
有四个.其中正确结论的个数有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com