
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,经过C作CD⊥AB于点D,CF是⊙O的切线,过点A作AE⊥CF于E,连接AC.
(1)求证:AE=AD.
(2)若AE=3,CD=4,求AB的长.

【答案】(1)证明见解析(2)![]()
【解析】
(1)连接OC,根据垂直定义和切线性质定理证出△CAE≌△CAD(AAS),得AE=AD;(2)连接CB,由(1)得AD=AE=3,根据勾股定理得:AC=5,由cos∠EAC=![]() ,cos∠CAB=
,cos∠CAB=![]() =
=![]() ,∠EAC=∠CAB,得
,∠EAC=∠CAB,得![]() =
=![]() .
.
(1)证明:连接OC,如图所示,
∵CD⊥AB,AE⊥CF,
∴∠AEC=∠ADC=90°,
∵CF是圆O的切线,
∴CO⊥CF,即∠ECO=90°,
∴AE∥OC,
∴∠EAC=∠ACO,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠EAC=∠CAO,
在△CAE和△CAD中,
 ,
,
∴△CAE≌△CAD(AAS),
∴AE=AD;
(2)解:连接CB,如图所示,
∵△CAE≌△CAD,AE=3,
∴AD=AE=3,
∴在Rt△ACD中,AD=3,CD=4,
根据勾股定理得:AC=5,
在Rt△AEC中,cos∠EAC=![]() =
=![]() ,
,
∵AB为直径,
∴∠ACB=90°,
∴cos∠CAB=![]() =
=![]() ,
,
∵∠EAC=∠CAB,
∴![]() =
=![]() ,即AB=
,即AB=![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】下面的网格中,每个小正方形的边长均为1个单位.小正方形的顶点叫做格点,以О点为原点,以过О点的水平直线MN为x轴建立平面直角坐标系.
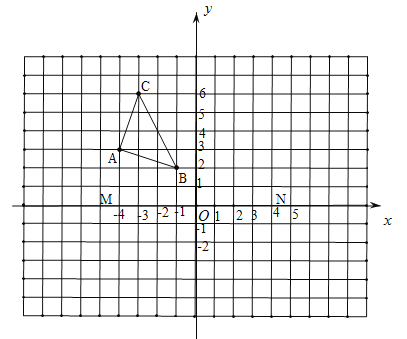
(1)![]() 与格点
与格点![]() 是关于y轴对称,画出
是关于y轴对称,画出![]() ;
;
(2)格点Р在第二象限内,且![]() 为等腰直角
为等腰直角![]() (注:P不在
(注:P不在![]() 的边上),画出
的边上),画出![]() ,并直接写出Р点坐标.
,并直接写出Р点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一抛物线形大门,其地面宽度![]() .一同学站在门内,在离门脚
.一同学站在门内,在离门脚![]() 点
点![]() 远的
远的![]() 处,垂直地面立
处,垂直地面立
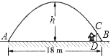
起一根![]() 长的木杆,其顶端恰好顶在抛物线形门上
长的木杆,其顶端恰好顶在抛物线形门上![]() 处.根据这些条件,请你求出该大门的高
处.根据这些条件,请你求出该大门的高![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图像与一正比例函数的图像相交于点
的图像与一正比例函数的图像相交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
(1)求正比例函数的解析式;
(2)若正比例函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像在第一象限内交于点
的图像在第一象限内交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,
轴的垂线,![]() 为垂足,且交直线
为垂足,且交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,
轴的垂线,![]() 为垂足,求梯形
为垂足,求梯形![]() 的面积;
的面积;
(3)连结![]() ,求
,求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD的边长是4,∠ABC=120°,点M、N分别在边AD、AB上,且MN⊥AC,垂足为P,把△AMN沿MN折叠得到△AˊMN,若△AˊDC恰为等腰三角形,则AP的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
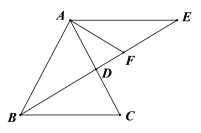
【题目】已知等腰△ABC中,AB=AC,∠ABC的平分线交AC于D,过点A作AE // BC交BD的延长线于点E,∠CAE的平分线交BE于点F.
(1)①如图,若∠BAC=36o,求证:BD=EF;
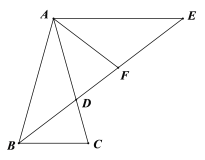
②如图,若∠BAC=60o,求![]() 的值;
的值;
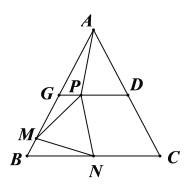
(2)如图,若∠BAC=60o,过点D作DG// BC,交AB于点G,点N为BC中点,点P, M分别是GD, BG上的动点,且∠PNM=60°. 求证:AP=PN=MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
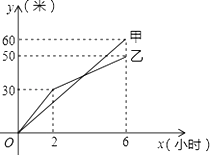
【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息有:①甲队挖掘30m时,用了3h;②挖掘6h时甲队比乙队多挖了10m;③乙队的挖掘速度总是小于甲队;④开挖后甲、乙两队所挖河渠长度相等时,x=4.其中一定正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+2的图象经过点A,且y随x的增大而减小.则A点的坐标可以是( )
A.(2,5)B.(﹣1,1)C.(3,0)D.(![]() ,4)
,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一品牌服装,销售一件可获利![]() 元,为在十一期间增加盈利,进行促销活动,决定采取降价措施.根据以往销售经验及市场调查发现,每件服装降价
元,为在十一期间增加盈利,进行促销活动,决定采取降价措施.根据以往销售经验及市场调查发现,每件服装降价![]() (元)与每天的销售量
(元)与每天的销售量![]() (件)之间的关系如下表
(件)之间的关系如下表
|
|
|
|
|
| … |
|
|
|
|
|
| … |
![]() 请你按照上表,求
请你按照上表,求![]() 与
与![]() 之间的函数解析式.
之间的函数解析式.
![]() 为保证每天能盈利
为保证每天能盈利![]() 元,又能吸引顾客,每件服装应降价多少元?
元,又能吸引顾客,每件服装应降价多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com