Question

【题目】下面的网格中，每个小正方形的边长均为1个单位．小正方形的顶点叫做格点，以О点为原点，以过О点的水平直线MN为x轴建立平面直角坐标系．

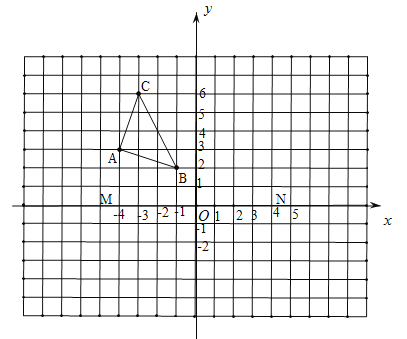
（1）与格点是关于y轴对称，画出；

（2）格点Р在第二象限内，且为等腰直角（注：P不在的边上），画出，并直接写出Р点坐标．

Answer 1

【答案】(1)见解析;(2) 图形见解析，

【解析】

（1）利用关于y轴对称点的性质得出对应点位置进而得出答案；

（2）易证△CAB是等腰直角三角形，且∠CAB=90°．然后分三种情况讨论即可得出结论．

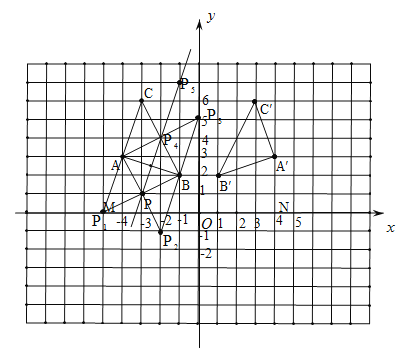
（1）如图所示：，即为所求；

（2）∵AC=，AB=，AC=，

AC2+AB2==10+10=20=BC2，

∴△CAB是等腰直角三角形，且∠CAB=90°．

分三种情况讨论：

①作C关于点A的对称点P1，则△BAP1是等腰直角三角形．设P1（x，y）．

∵A（－4，3），C（－3，6），

∴－3+x=2×（－4），6+y=2×3，

解得：x=－3，y=0，

∴P1（－3，0），点P1在x轴上，不符合题意，舍去．

②以B为旋转中心，把BA绕B点逆时针旋转90°得到P2，把BA绕B点顺时针旋转90°得到P3，易得P2（－2，－1）在第三象限，P3（0，5）在y轴上，都不符合题意，舍去；

③作AB的垂直平分线．在第二象限内AB的垂直平分线上有三个格点P、P4、P5．

∵P4在BC上，∴P4不合题意．

∵△ABP5不是直角三角形，∴P5不合题意．

∵AP=，BP=，AB=，

∴AP=BP，AP2+BP2==5+5=10=AB2，

∴∠APB=90°，∴△APB是等腰直角三角形，∴点P满足条件．

由图可知：点P的坐标为P（－3，1）．