
【题目】如图,已知抛物线y=ax2﹣5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.

(1)求抛物线的解析式;
(2)求直线BC的解析式;
(3)若点N是抛物线上的动点,且点N在第四象限内,过点N作NH⊥x轴,垂足为H,以B,N,H为顶点的三角形是否能够与△OBC相似?若能,请求出所有符合条件点N的坐标;若不能,请说明理由.
【答案】(1)y=![]() x2﹣5ax+2;(2)y=﹣
x2﹣5ax+2;(2)y=﹣![]() x+2;(3)(2,-1)
x+2;(3)(2,-1)
【解析】
试题分析:(1)把点A(1,0)在抛物线y=ax2﹣5ax+2上,解方程即可得到结论;
(2)把x=0代入y=![]() x2﹣5ax+2,求得C(0,2),根据抛物线的对称轴为直线x=
x2﹣5ax+2,求得C(0,2),根据抛物线的对称轴为直线x=![]() ,得到B(4,0),求出直线BC的解析式y=﹣
,得到B(4,0),求出直线BC的解析式y=﹣![]() x+2;
x+2;
(3)设N(x,![]() x2﹣
x2﹣![]() x+2),根据相似三角形的性质得到
x+2),根据相似三角形的性质得到![]() ,即可得到结论.
,即可得到结论.
试题解析:(1)∵点A(1,0)在抛物线y=ax2﹣5ax+2上,
∴a﹣5a+2=0,∴a=![]() ,
,
∴抛物线的解析式为:y=![]() x2﹣5ax+2;
x2﹣5ax+2;
(2)把x=0代入y=![]() x2﹣5ax+2,
x2﹣5ax+2,
解得:y=2,
∴C(0,2),
∵抛物线的对称轴为直线x=![]() ,
,
∴B(4,0),
设直线BC的解析式为:y=kx+b,
∴![]() ,
,
解得:k=﹣![]() ,b=2,
,b=2,
∴直线BC的解析式为:y=﹣![]() x+2;
x+2;
(3)设N(x,![]() x2﹣
x2﹣![]() x+2),
x+2),
当△OBC∽△HBN时,如图,
∴![]() ,
,
即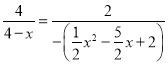 ,
,
解得:x1=2,x2=4(不合题意舍去)
故N的坐标为(2,-1)


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】某商场6月份随即调查了6天的营业额,结果分别如下(单位:万元):2.8,3.2,3.4,3.0,3.1,3.7,试估算该商场6月份总营业额大约是( )
A. 84万元 B. 96万元
C. 93万元 D. 111万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中∠A=90°,∠A,∠B,∠C的对边分别为a,b,c,则( )
A. a2+b2=c2B. b2+c2=a2C. a2+c2=b2D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程x2+4x+1=0,配方后的方程是( )
A. (x+2)2=3 B. (x﹣2)2=3 C. (x﹣2)2=5 D. (x+2)2=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=8cm,BC=4cm,AB=5cm.从初始时刻开始,动点P,Q 分别从点A,B同时出发,运动速度均为1cm/s,动点P沿A﹣B﹣﹣C﹣﹣E的方向运动,到点E停止;动点Q沿B﹣﹣C﹣﹣E﹣﹣D的方向运动,到点D停止,设运动时间为xs,△PAQ的面积为ycm2,(这里规定:线段是面积为0的三角形)
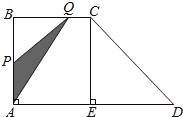
解答下列问题:
(1)当x=2s时,y= cm2;当x=![]() s时,y= cm2.
s时,y= cm2.
(2)当5≤x≤14 时,求y与x之间的函数关系式.
(3)当动点P在线段BC上运动时,求出![]() 时x的值.
时x的值.
(4)直接写出在整个运动过程中,使PQ与四边形ABCE的对角线平行的所有x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com