
【题目】如图所示,1925年数学家莫伦发现的世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形,其中标注1、2的正方形边长分别为x、y,请你计算: 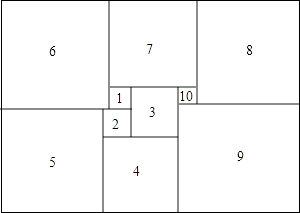
(1)第3个正方形的边长=;第5个正方形的边长=;第10个正方形的边长= . (用含x、y的代数式表示)
(2)当x=2时,第9个正方形的面积= .
(3)当x、y均为正整数时,求这个完美长方形的最小周长.
【答案】
(1)x+y;x+3y;3y﹣3x
(2)100
(3)解:假设正方形1的边长为x,正方形2的边长为y,正方形3的边长为x+y,正方形4的边长为x+2y,正方形5的边长为x+3y,正方形6的边长x+3y+(y﹣x)=4y,正方形7的边长为4y﹣x,正方形8的边长为4y﹣x+3y﹣3x=7y﹣4x,正方形9的边长为10y﹣7x,正方形10的边长为4y﹣x﹣x﹣x﹣y=3y﹣3x,完美长方形存在如下关系 x+3y+4y=7y﹣4x+10y﹣7x 即可得出y=1.2x
完美长方形周长=2(x+3y+4y+x+2y+x+3y+10y﹣7x)=2(22y﹣4x)=44.8x
由于xy均为正整数,所以x=5,y=6,此时完美长方形的周长为44.8x=44.8×5=224.
答:这个完美长方形的最小周长为224
【解析】解:(1)第1、2的正方形边长分别为x、y,则第3个正方形的边长=x+y;第4个正方形的边长=x+y+y=x+2y;第5个正方形的边长=x+2y+y=x+3y;第6正方形的边长=x+3y+y﹣x=4y;第7正方形的边长=4y﹣x;第10正方形的边长=4y﹣x﹣﹣x(x+y)=3y﹣3x;
所以答案是:x+y,x+3y,3y﹣3x.(2)第9正方形的边长=x+y+x+2y﹣(3y﹣3x)=5x,
当x=2时,第9正方形的边长=5x=10,
所以第9正方形的面积为100;
所以答案是:100(3)假设正方形1的边长为x,正方形2的边长为y,正方形3的边长为x+y,正方形4的边长为x+2y,正方形5的边长为x+3y,正方形6的边长x+3y+(y﹣x)=4y,正方形7的边长为4y﹣x,正方形8的边长为4y﹣x+3y﹣3x=7y﹣4x,正方形9的边长为10y﹣7x,正方形10的边长为4y﹣x﹣x﹣x﹣y=3y﹣3x,完美长方形存在如下关系 x+3y+4y=7y﹣4x+10y﹣7x 即可得出y=1.2x
完美长方形周长=2(x+3y+4y+x+2y+x+3y+10y﹣7x)=2(22y﹣4x)=44.8x
由于xy均为正整数,所以x=5,y=6,此时完美长方形的周长为44.8x=44.8×5=224.
答:这个完美长方形的最小周长为224
【考点精析】解答此题的关键在于理解代数式求值的相关知识,掌握求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
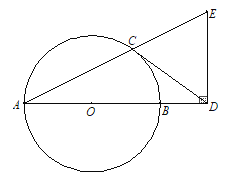
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB=![]() ,AB=3,求BD的长.
,AB=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表:
| 甲 | 乙 |
原料成本 | 12 | 8 |
销售单价 | 18 | 12 |
生产提成 | 1 | 0.8 |
(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入﹣投入总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年“龙岗年货博览会”在大运中心体育馆展销,小丽从家出发前去购物,途中发现忘了带钱,于是打电话让妈妈马上从家里送来,同时小丽也往回走,遇到妈妈后聊了一会儿,接着继续前往大运中心体育馆.设小丽从家出发后所用时间为t,小丽与体育馆的距离为S,下面能反映S与t的函数关系的大致图象是( )
A.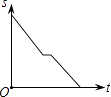
B.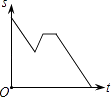
C.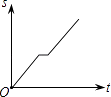
D.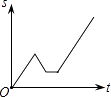
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题。
(1)定义新运算:对于任意有理数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算,比如,数字2和5在该新运算下结果为﹣5.计算如下:
2⊕5=2×(2﹣5)+1
=2×(﹣3)+1
=﹣6+1
=﹣5
求(﹣2)⊕3的值;
(2)对于有理数a、b,若定义运算:ab= ![]() (﹣4)3的值等于
(﹣4)3的值等于
(3)请你定义一种新运算,使得数字﹣4和6在你定义的新运算下结果为20.写出你定义的新运算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)(﹣7)﹣(﹣10)+(﹣8)﹣(+2)
(2)﹣6÷(﹣ ![]() )×
)× ![]()
(3)( ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )×105
)×105
(4)﹣14+[1﹣(1﹣0.5× ![]() )]×[2﹣(﹣3)2].
)]×[2﹣(﹣3)2].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com