【题目】如图1，△ABC是等腰直角三角形，∠BAC=90°，AB=AC，四边形ADEF是正方形，点B、C分别在边AD、AF上，此时BD=CF，BD⊥CF成立．

（1）当△ABC绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明，若不成立，请说明理由；

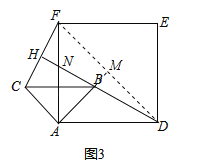
（2）当△ABC绕点A逆时针旋转45°时，如图3，延长BD交CF于点H．

①求证：BD⊥CF；

②当AB=2，AD=时，求线段DH的长．

参考答案：

【答案】（1）BD=CF；（2）①证明见解析；②．

【解析】分析：（1）根据旋转变换的性质和全等三角形的判定定理证明△CAF≌△BAD，证明结论；

（2）①根据全等三角形的性质、垂直的定义证明即可；

②连接DF，延长AB交DF于M，根据题意和等腰直角三角形的性质求出DM、BM的长，根据勾股定理求出BD的长，根据相似三角形的性质列出比例式，计算即可得到答案．

（1）BD=CF．

理由如下：由题意得，∠CAF=∠BAD=θ，在△CAF和△BAD中，∵CA=BA，∠CAF=∠BAD，FA=DA，∴△CAF≌△BAD，∴BD=CF；

（2）①由（1）得△CAF≌△BAD，∴∠CFA=∠BDA，∵∠FNH=∠DNA，∠DNA+∠NAD=90°，∴∠CFA+∠FNH=90°，∴∠FHN=90°，即BD⊥CF；

②连接DF，延长AB交DF于M，∵四边形ADEF是正方形，AD=，AB=2，∴AM=DM=3，BM=AM﹣AB=1，∵△ABC绕点A逆时针旋转45°，∴∠BAD=45°，∴AM⊥DF，∴DB==，∵∠MAD=∠MDA=45°，∴∠AMD=90°，又∠DHF=90°，∠MDB=∠HDF，∴△DMB∽△DHF，∴，即，解得，DH=．

关闭