
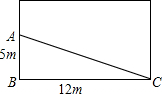
 如图,长方形的花圃中,有人避开拐角线A→B→C而直接走“捷径”AC,小明想在A处树立一个标牌“少走4米,踏之何忍”,请根据图中数字计算完成标牌中未填的数字.
如图,长方形的花圃中,有人避开拐角线A→B→C而直接走“捷径”AC,小明想在A处树立一个标牌“少走4米,踏之何忍”,请根据图中数字计算完成标牌中未填的数字.  世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
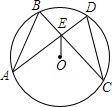 如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知$\widehat{AB}$=$\widehat{CD}$.
如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知$\widehat{AB}$=$\widehat{CD}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
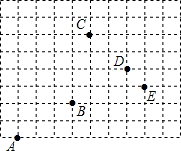 如图,用(1,0)表示A点的位置,那么:
如图,用(1,0)表示A点的位置,那么:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com