
【题目】某商店经销一种双肩包,已知这种双肩包的成本价每个20元,市场调查发现,这种双肩包每天的销售量![]() (单位:个)与销售单价
(单位:个)与销售单价![]() (单位:元)有如下关系:
(单位:元)有如下关系:![]() (
(![]() )设这种双肩包每天的销售利润为
)设这种双肩包每天的销售利润为![]() 元.
元.
(1)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(2)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得300元的销售利润,销售单价应定为多少元?
【答案】(1)当![]() 时,
时,![]() 有最大值,最大值是400;(2)该商店销售这种双肩包每天要获得300元的销售利润,销售单价应定为30元.
有最大值,最大值是400;(2)该商店销售这种双肩包每天要获得300元的销售利润,销售单价应定为30元.
【解析】
(1)根据“利润=单件利润![]() 销售量”建立等式,再利用二次函数的性质求解即可;
销售量”建立等式,再利用二次函数的性质求解即可;
(2)根据题(1)的w与x的函数解析式,令![]() 得到一个一元二次方程,再结合
得到一个一元二次方程,再结合![]() 的要求,求解即可.
的要求,求解即可.
(1)由题意得:![]()
则![]() 与
与![]() 之间的函数解析式
之间的函数解析式![]()
整理得:![]()
由二次函数的性质可知:当![]() 时,w随x的增大而增大;当
时,w随x的增大而增大;当![]() 时,w随x的增大而减小
时,w随x的增大而减小
则当![]() 时,
时,![]() 取得最大值,最大值是400
取得最大值,最大值是400
答:这种双肩包销售单价定为40元时,每天的销售利润最大,最大利润是400元;
(2)当![]() 时,
时,![]()
解得:![]()
因![]() ,故
,故![]() 不符合题意,舍去
不符合题意,舍去
答:该商店销售这种双肩包每天要获得300元的销售利润,销售单价应定为30元.


科目:初中数学 来源: 题型:
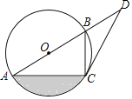
【题目】如图,已知AB是⊙O的直径,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.
(1)求证:CD是⊙O的切线.
(2)若∠D=30°,BD=2,求⊙O的半径
(3)在(2)的条件下,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】斗门某养殖户每年的养殖成本包括固定成本和可变动成本,其中固定成本每年均为4万元,可变动成本逐年增长. 已知该养殖户第1年的可变动成本为2万元,设可变动成本的年平均增长率为x.
(1)用含x的代数式表示第2年的可变动成本: 万元;
(2)如果该养殖户第3年的成本为6.42万元,求可变动成本的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国长江、黄河流域植被遭到破坏,导致土地沙化,洪涝灾害时有发生、沿黄某地区为积极响应和支持“保护母亲河”的倡议,在2000年建立了长100km,宽0.5km的防护林、今年,有关部门为统计这一防护林约有多少棵树,从中选出10块(每块长1km,宽0.5km)统计,数量如下(单位:棵):65110 63200 64600 64700 67300 63300 65100 66600 62800 65500,根据以上数据可知这一防护林约有_____棵树.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,抛物线
,抛物线![]()
![]() 经过点
经过点![]() ,将点
,将点![]() 向右平移5个单位长度,得到点
向右平移5个单位长度,得到点![]() ,若抛物线与线段
,若抛物线与线段![]() 恰有一个公共点,结合函数图象,则
恰有一个公共点,结合函数图象,则![]() 的取值范围__________.
的取值范围__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,t=![]() 或
或![]() .
.
其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
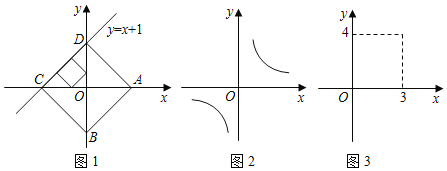
【题目】已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A.B.C.D各点依次排列)为正方形时,我们称这个正方形为此函数图象的“和谐正方形”.例如:在图1中,正方形ABCD是一次函数y=x+1图象的其中一个“和谐正方形”.
(1)如图1,若某函数是一次函数y=x+1,求它的图象的所有“和谐正方形”的边长;
(2)如图2,若某函数是反比例函数y=![]() (k>0),它的图象的“和谐正方形”为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数的解析式;
(k>0),它的图象的“和谐正方形”为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数的解析式;
(3)如图3,若某函数是二次函数y=ax2+c(a≠0),它的图象的“和谐正方形”为ABCD,C、D中的一个点坐标为(3,4),请求出该二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如图所示(单位:cm),则该铁球的直径为( )
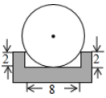
A.12 cmB.10 cmC.8 cmD.6 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图a,AB为⊙O直径,AC为⊙O的为弦,PA为⊙O的切线,∠APC=2∠1.
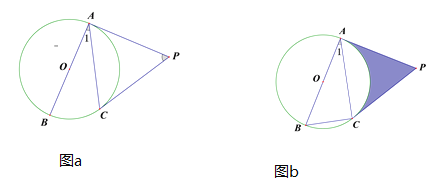
(1)求证:PC是⊙O的切线.
(2)当∠1=30°,AB=4时,其他条件不变,求图b中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com