
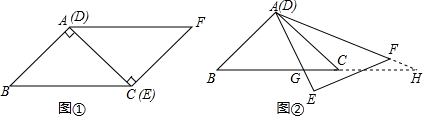
分析 采用分类讨论的思想,当CG<$\frac{1}{2}$BC时,当CG=$\frac{1}{2}$BC时,当CG>$\frac{1}{2}$BC时分别得出即可.
解答  解:①当CG<$\frac{1}{2}$BC时,∠GAC=∠H<∠HAC,
解:①当CG<$\frac{1}{2}$BC时,∠GAC=∠H<∠HAC,
∴AC<CH,
∵AG<AC,
∴AG<CH<GH,
又∵AH>AG,AH>GH,
此时,△AGH不可能是等腰三角形;
②当CG=$\frac{1}{2}$BC时,G为BC的中点,H与C重合,△AGH是等腰三角形,
此时,GC=$\frac{9\sqrt{2}}{2}$;
③当CG>$\frac{1}{2}$BC时,由(1)△AGC∽△HGA,
若△AGH必是等腰三角形,只可能存在GH=AH,若G′H=AH,则AC=CG′,此时x=9,
如图,当CG′=BC时,
注意:DF才旋转到与BC垂直的位置,
此时B,E,G重合,∠AG′H=∠G′AH=45°,
∴△AG′H为等腰三角形,所以CG′=9$\sqrt{2}$.
综上所述,当CG的长为9或$\frac{9\sqrt{2}}{2}$或9$\sqrt{2}$时,△AGH是等腰三角形.
故答案为:9或$\frac{9\sqrt{2}}{2}$或9$\sqrt{2}$.
点评 此题主要考查了等腰三角形的性质、等腰直角三角形的性质、旋转的性质等知识,正确利用分类讨论得出是解题关键.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
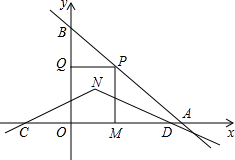 如图,在平面直角坐标系中,直线y=-x+6交x轴于点A,交y轴于点B,点P为直线AB上一动点,过点P作PM⊥x轴于点M,PQ⊥y轴于点Q,点P的横坐标为m,∠CND的两边NC的解析式为y=$\frac{x}{2}$+m-$\frac{1}{2}$,边ND的解析式为y=-$\frac{x}{2}$+m+$\frac{1}{2}$,也随点P的运动而变化,其顶点为点N.
如图,在平面直角坐标系中,直线y=-x+6交x轴于点A,交y轴于点B,点P为直线AB上一动点,过点P作PM⊥x轴于点M,PQ⊥y轴于点Q,点P的横坐标为m,∠CND的两边NC的解析式为y=$\frac{x}{2}$+m-$\frac{1}{2}$,边ND的解析式为y=-$\frac{x}{2}$+m+$\frac{1}{2}$,也随点P的运动而变化,其顶点为点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
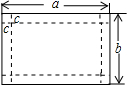 如图是一个长、宽分别为a,b的长方形铁皮,在铁皮的四角各剪去一个边长为c的正方形(2c<b<a),然后做成一个无盖的长方体盒子.
如图是一个长、宽分别为a,b的长方形铁皮,在铁皮的四角各剪去一个边长为c的正方形(2c<b<a),然后做成一个无盖的长方体盒子.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
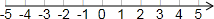 已知在纸面上有一数轴(如下图),折叠纸面.
已知在纸面上有一数轴(如下图),折叠纸面. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com