
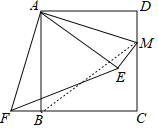
【题目】如图,在正方形ABCD中,AB=5,点M在CD的边上,且DM=2,△AEM与△ADM关于AM所在的直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
连接BM.先判定△FAE≌△MAB(SAS),即可得到EF=BM.再根据BC=CD=AB=5,CM=3,利用勾股定理即可得到,Rt△BCM中,BM=![]() ,进而得出EF的长.
,进而得出EF的长.
解:如图,连接BM.
∵△AEM与△ADM关于AM所在的直线对称,
∴AE=AD,∠MAD=∠MAE.
∵△ADM按照顺时针方向绕点A旋转90°得到△ABF,
∴AF=AM,∠FAB=∠MAD.
∴∠FAB=∠MAE
∴∠FAB+∠BAE=∠BAE+∠MAE.
∴∠FAE=∠MAB.
∴△FAE≌△MAB(SAS).
∴EF=BM.
∵四边形ABCD是正方形,
∴BC=CD=AB=5.
∵DM=2,
∴CM=3.
∴在Rt△BCM中,BM=![]() ,
,
∴EF=![]() ,
,
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,无人机在空中C处测得地面A、B两点的俯角分别为60°、45°,如果无人机距地面高度CD为![]() 米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)
米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三台县教育和体育局为帮助万福村李大爷“精准脱贫”,在网上销售李大爷自己手工做的竹帘,其成本为每张40元,当售价为每张80元时,每月可销售100张.为了吸引更多顾客,采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5张.设每张竹帘的售价为![]() 元(
元(![]() 为正整数),每月的销售量为
为正整数),每月的销售量为![]() 张.
张.
(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设该网店每月获得的利润为![]() 元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)李大爷深感扶贫政策给自己带来的好处,为了回报社会,他决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,求销售单价应该定在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3)在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出x的值大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
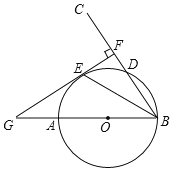
【题目】如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且![]() =
=![]() ,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
(1)证明:GF是⊙O的切线;
(2)若AG=6,GE=6![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“衍生直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“衍生三角形”.已知抛物线![]() 与其“衍生直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“衍生直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.

(1)填空:该抛物线的“衍生直线”的解析式为 ,点A的坐标为 ,点B的坐标为 ;
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“衍生三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“衍生直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
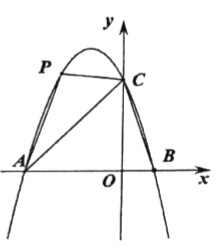
【题目】如图,抛物线![]() 经过
经过![]() 三点
三点
(1)求抛物线的解析式;
(2)在直线![]() 上方的抛物线上是否存在一点
上方的抛物线上是否存在一点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的一半?若存在,求出点
的面积的一半?若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(3)点![]() 为抛物线上一动点,在
为抛物线上一动点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,求出点
为顶点的四边形是平行四边形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com