
分析 (1)①根据题意补全图形即可;②根据旋转的性质,即可解答;
(2)线段CM,AE和BE之间的数量关系是AE=BE+2CM,理由如下:根据旋转的性质,证明A、D、E三点在同一条直线上,得到AE=AD+DE.再证明△ACD≌△BCE,得到AD=BE.又CD=CE,∠DCE=90°,CM⊥DE,得到DE=2CM,所以AE=BE+2CM.
(3)由PD=1可得:点P在以点D为圆心,1为半径的圆上;由∠BPD=90°可得:点P在以BD为直径的圆上.显然,点P是这两个圆的交点,由于两圆有两个交点,接下来需对两个位置分别进行讨论.然后,添加适当的辅助线,借助于(2)中的结论即可解决问题.
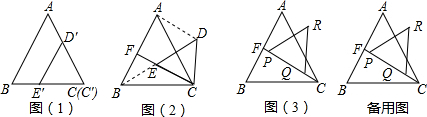
解答 解:(1)①如图所示: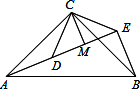
②∠ADC+∠CDE=180°.
(2)线段CM,AE和BE之间的数量关系是AE=BE+2CM,理由如下:
∵线段CD绕点C逆时针旋转90°得到线段CE,
∴CD=CE,∠DCE=90°.
∴∠CDE=∠CED=45°.
又∵∠ADC=135°,
∴∠ADC+∠CDE=180°,
∴A、D、E三点在同一条直线上.
∴AE=AD+DE.
又∵∠ACB=90°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE.
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$
∴△ACD≌△BCE.
∴AD=BE.
∵CD=CE,∠DCE=90°,CM⊥DE.
∴DE=2CM.
∴AE=BE+2CM.
(3)点A到BP的距离为$\frac{\sqrt{3}+1}{2}$或$\frac{\sqrt{3}-1}{2}$.
理由如下:
∵PD=1,
∴点P在以点D为圆心,1为半径的圆上.
∵∠BPD=90°,
∴点P在以BD为直径的圆上.
∴点P是这两圆的交点.
①当点P在如图3①所示位置时,
连接PD、PB、PA,作AH⊥BP,垂足为H,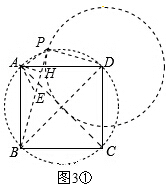
过点A作AE⊥AP,交BP于点E,如图3①.
∵四边形ABCD是正方形,
∴∠ADB=45°.AB=AD=DC=BC=$\sqrt{2}$,∠BAD=90°.
∴BD=2.
∵DP=1,
∴BP=$\sqrt{3}$.
∵∠BPD=∠BAD=90°,
∴A、P、D、B在以BD为直径的圆上,
∴∠APB=∠ADB=45°.
∴△PAE是等腰直角三角形.
又∵△BAD是等腰直角三角形,点B、E、P共线,AH⊥BP,
∴由(2)中的结论可得:BP=2AH+PD.
∴$\sqrt{3}$=2AH+1.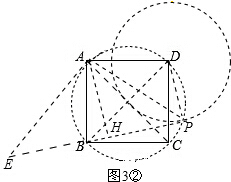
∴AH=$\frac{\sqrt{3}-1}{2}$.
②当点P在如图3②所示位置时,
连接PD、PB、PA,作AH⊥BP,垂足为H,
过点A作AE⊥AP,交PB的延长线于点E,如图3②.
同理可得:BP=2AH-PD.
∴$\sqrt{3}$=2AH-1.
∴AH=$\frac{\sqrt{3}+1}{2}$.
综上所述:点A到BP的距离为$\frac{\sqrt{3}-1}{2}$或$\frac{\sqrt{3}+1}{2}$.
点评 本题考查了等边三角形的性质、正方形的性质、等腰三角形的性质、直角三角形斜边上的中线等于斜边的一半、圆周角定理、三角形全等的判定与性质等知识,考查了运用已有的知识和经验解决问题的能力,是体现新课程理念的一道好题.而通过添加适当的辅助线从而能用(2)中的结论解决问题是解决第(3)的关键.


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
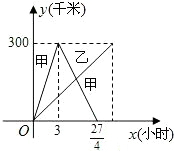 已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数$y=\frac{k}{x}$(x>0)的图象与△线段CB、CA都相交,则k的取值范围是( )
如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数$y=\frac{k}{x}$(x>0)的图象与△线段CB、CA都相交,则k的取值范围是( )| A. | 2≤k≤4 | B. | 2≤k≤5 | C. | 2≤k≤8 | D. | 5≤k≤8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
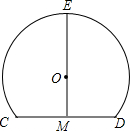 一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E.若CD=6,则隧道的高(ME的长)为( )
一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E.若CD=6,则隧道的高(ME的长)为( )| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
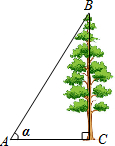 如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )| A. | 6sin75°米 | B. | $\frac{6}{cos75°}$米 | C. | $\frac{6}{tan75°}$米 | D. | 6tan75°米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com