
【题目】如图,已知一张长方形纸片,![]() (
(![]() ).将这张纸片沿着过点
).将这张纸片沿着过点![]() 的折痕翻折,使点
的折痕翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() ,折痕交
,折痕交![]() 于点
于点![]() ,将折叠后的纸片再次沿着另一条过点
,将折叠后的纸片再次沿着另一条过点![]() 的折痕翻折,点
的折痕翻折,点![]() 恰好与点
恰好与点![]() 重合,此时折痕交
重合,此时折痕交![]() 于点
于点![]() .
.
(1)在图中确定点![]() 、点
、点![]() 和点
和点![]() 的位置;
的位置;
(2)联结![]() ,则
,则![]() ______
______![]() ;
;
(3)用含有![]() 的代数式表示线段
的代数式表示线段![]() 的长.(注:直角三角形中,两直角边的平方的和等于斜边的平方)
的长.(注:直角三角形中,两直角边的平方的和等于斜边的平方)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
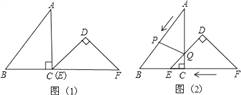
【题目】已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上,∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=9cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿BA匀速移动,当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动,DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).
解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式,是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由;
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOD=160°,OB、OC、OM、ON是∠AOD内的射线.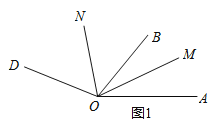
(1)如图1,若OM平分∠AOB,ON平分∠BOD.当OB绕点O在∠AOD内旋转时,求∠MON的大小;
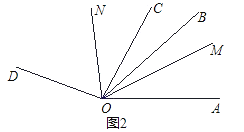
(2)如图2,若∠BOC=20°,OM平分∠AOC,ON平分∠BOD.当∠BOC绕点O在∠AOD内旋转时,求∠MON的大小;
(3)在(2)的条件下,若∠AOB=10°,当∠B0C在∠AOD内绕着点O以2度/秒的速度逆时针旋转t秒时,∠AOM=![]() ∠DON.求t的值.
∠DON.求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两块大小不等的等腰直角三角形按图1放置,点![]() 为直角顶点,点
为直角顶点,点![]() 在
在![]() 上,将
上,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 角度
角度![]() ,连接
,连接![]() 、
、![]() .
.
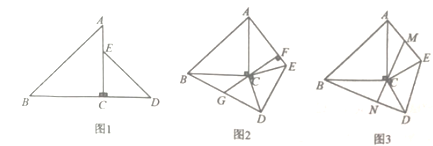
(1)若![]() ,则当
,则当![]()
![]() 时,四边形
时,四边形![]() 是平行四边形;
是平行四边形;
(2)图2,若![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() 是
是![]() 的中点;
的中点;
(3)图3,若点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.

若某户居民![]() 月份用水
月份用水![]() ,则应收水费:
,则应收水费:![]() 元.
元.
(1)若该户居民![]() 月份用水
月份用水![]() ,则应收水费______元;
,则应收水费______元;
(2)若该户居民![]() 、
、![]() 月份共用水
月份共用水![]() (
(![]() 月份用水量超过
月份用水量超过![]() 月份),共交水费
月份),共交水费![]() 元,则该户居民
元,则该户居民![]() ,
,![]() 月份各用水多少立方米?
月份各用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=﹣![]() x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=
x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=![]() MP,MB=
MP,MB=![]() OM,OE=
OM,OE=![]() ON,ND=
ON,ND=![]() NP.
NP.
(1)b= ;
(2)求证:四边形BCDE是平行四边形;
(3)在直线y=﹣![]() x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.
x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华将一条直角边长为1的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到一个等腰直角三角形(如图3),则图3中的等腰直角三角形的一条腰长为_________;同上操作,若小华连续将图1的等腰直角三角形折叠n次后所得到的等腰直角三角形(如图n+1)的一腰长为_________.
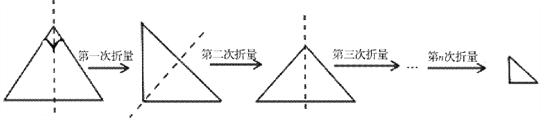
图1 图2 图3 图n+1
查看答案和解析>>
科目:初中数学 来源: 题型:
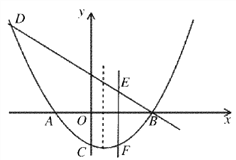
【题目】如图,已知拋物线![]() (k为常数,且k>0)与x轴的交点为A、B,与y轴的交点为C,经过点B的直线
(k为常数,且k>0)与x轴的交点为A、B,与y轴的交点为C,经过点B的直线![]() 与抛物线的另一个交点为D.
与抛物线的另一个交点为D.
(1)若点D的横坐标为x= -4,求这个一次函数与抛物线的解析式;
(2)若直线m平行于该抛物线的对称轴,并且可以在线段AB间左右移动,它与直线BD和抛物线分别交于点E、F,求当m移动到什么位置时,EF的值最大,最大值是多少?
(3)问原抛物线在第一象限是否存在点P,使得△APB∽△ABC?若存在,请求出这时k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距480km,C地在A、B两地之间.一辆轿车以100km/h的速度从A地出发匀速行驶,前往B地.同时,一辆货车以80km/h的速度从B地岀发,匀速行驶,前往A地.
(1)当两车相遇时,求轿车行驶的时间;
(2)当两车相距120km时,求轿车行驶的时间;
(3)若轿车到达B地后,立刻以120km/h的速度原路返回,再次经过C地,两次经过C地的时间间隔为2.2h,求C地距离A地路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com