
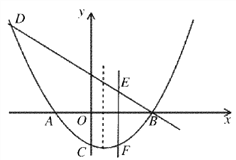
【题目】如图,已知拋物线![]() (k为常数,且k>0)与x轴的交点为A、B,与y轴的交点为C,经过点B的直线
(k为常数,且k>0)与x轴的交点为A、B,与y轴的交点为C,经过点B的直线![]() 与抛物线的另一个交点为D.
与抛物线的另一个交点为D.
(1)若点D的横坐标为x= -4,求这个一次函数与抛物线的解析式;
(2)若直线m平行于该抛物线的对称轴,并且可以在线段AB间左右移动,它与直线BD和抛物线分别交于点E、F,求当m移动到什么位置时,EF的值最大,最大值是多少?
(3)问原抛物线在第一象限是否存在点P,使得△APB∽△ABC?若存在,请求出这时k的值;若不存在,请说明理由.
【答案】(1) ![]() (2) 最大值是4(3)存在
(2) 最大值是4(3)存在
【解析】分析:(1)先解方程k(x+2)(x﹣4)=0可得A(﹣2,0),B(4,0),再把B点坐标代入y=﹣![]() x+b中求出得b=2,则可得到一次函数解析式为y=﹣
x+b中求出得b=2,则可得到一次函数解析式为y=﹣![]() x+2,接着利用一次函数解析式确定D点坐标,然后把D点坐标代入代入y=k(x+2)(x﹣4)中求出k的值即可得到得抛物线解析式;
x+2,接着利用一次函数解析式确定D点坐标,然后把D点坐标代入代入y=k(x+2)(x﹣4)中求出k的值即可得到得抛物线解析式;
(2)利用二次函数和一次函数图象上点的坐标特征,可设F(t,![]() t2﹣
t2﹣![]() t﹣2),则E(t,﹣
t﹣2),则E(t,﹣![]() t+2),﹣2≤t≤4,于是得到EF=﹣
t+2),﹣2≤t≤4,于是得到EF=﹣![]() t+2﹣(
t+2﹣(![]() t2﹣
t2﹣![]() t﹣2)=﹣
t﹣2)=﹣![]() t2+4,然后根据二次函数的性质求解;
t2+4,然后根据二次函数的性质求解;
(3)作PH⊥x轴于H,如图,先表示出C点坐标为(0,﹣8k),设P[n,k(n+2)(n﹣4)],根据相似三角形的判定方法,当∠PAB=∠CAB,AP:AB=AB:AC时,△APB∽△ABC;再根据正切定义.在Rt△APH中有tan∠PAH=![]() .在Rt△OAC中有tan∠OAC=
.在Rt△OAC中有tan∠OAC=![]() =4k,则
=4k,则![]() =4k,解得n=8,于是得到P(8,40k),接着利用勾股定理计算出AP=10
=4k,解得n=8,于是得到P(8,40k),接着利用勾股定理计算出AP=10![]() ,AC=2
,AC=2![]() ,然后利用AP:AB=AB:AC得到10
,然后利用AP:AB=AB:AC得到10![]() 2
2=62,解得k1=
![]() ,k2=﹣
,k2=﹣![]() (舍去),于是可确定P点坐标.
(舍去),于是可确定P点坐标.
详解:(1)当y=0时,k(x+2)(x﹣4)=0,解得:x1=﹣2,x2=4,则A(﹣2,0),B(4,0),把B(4,0)代入y=﹣![]() x+b得:﹣2+b=0,解得:b=2,所以一次函数解析式为y=﹣
x+b得:﹣2+b=0,解得:b=2,所以一次函数解析式为y=﹣![]() x+2,当x=﹣4时,y=﹣
x+2,当x=﹣4时,y=﹣![]() x+2=4,则D点坐标为(4,4),把D(﹣4,4)代入y=k(x+2)(x﹣4)得:k(﹣2)(﹣8)=4,解得:k=
x+2=4,则D点坐标为(4,4),把D(﹣4,4)代入y=k(x+2)(x﹣4)得:k(﹣2)(﹣8)=4,解得:k=![]() ,所以抛物线解析式为y=
,所以抛物线解析式为y=![]() (x+2)(x﹣4),即y=
(x+2)(x﹣4),即y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)设F(t,![]() t2﹣
t2﹣![]() t﹣2),则E(t,﹣
t﹣2),则E(t,﹣![]() t+2),﹣2≤t≤4,所以EF=﹣
t+2),﹣2≤t≤4,所以EF=﹣![]() t+2﹣(
t+2﹣(![]() t2﹣
t2﹣![]() t﹣2)=﹣
t﹣2)=﹣![]() t2+4,所以当t=0时,EF最大,最大值为4,即当直线m移动到与y轴重合的位置时,EF的值最大,最大值是4;
t2+4,所以当t=0时,EF最大,最大值为4,即当直线m移动到与y轴重合的位置时,EF的值最大,最大值是4;
(3)存在.
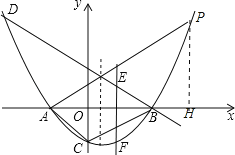
作PH⊥x轴于H,如图,当x=0时,y=k(x+2)(x﹣4)=﹣8k,则C(0,﹣8k),设P[n,k(n+2)(n﹣4)],当∠PAB=∠CAB,AP:AB=AB:AC时,△APB∽△ABC;
在Rt△APH中,tan∠PAH=![]() .在Rt△OAC中,tan∠OAC=
.在Rt△OAC中,tan∠OAC=![]() =4k,∴
=4k,∴![]() =4k,解得:n=8,则P(8,40k),∴AP=
=4k,解得:n=8,则P(8,40k),∴AP=![]() =
=![]() =10
=10![]() ,而AC=
,而AC=![]() =
=![]() =2
=2![]() .∵AP:AB=AB:AC,∴APAC=AB2,即10
.∵AP:AB=AB:AC,∴APAC=AB2,即10![]() 2
2![]() =62,∴5(16k2+1)=9,解得:k1=
=62,∴5(16k2+1)=9,解得:k1=![]() ,k2=﹣
,k2=﹣![]() (舍去),∴k=4
(舍去),∴k=4![]() ,P点坐标为(8,4
,P点坐标为(8,4![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
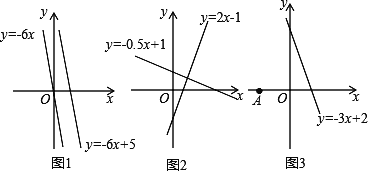
【题目】材料一:如图1,由课本91页例2画函数y=﹣6x与y=﹣6x+5可知,直线y=﹣6x+5可以由直线y=﹣6x向上平移5个单位长度得到由此我们得到正确的结论一:在直线L1:y=K1x+b1与直线L2:y=K2x+b2中,如果K1=K2 且b1≠b2 ,那么L1∥L2,反过来,也成立.
材料二:如图2,由课本92页例3画函数y=2x﹣1与y=﹣0.5x+1可知,利用所学知识一定能证出这两条直线是互相垂直的.由此我们得到正确的结论二:在直线L1:y=k1x+b1 与L2:y=k2x+b2 中,如果k1·k2=-1那么L1⊥L2,反过来,也成立
应用举例
已知直线y=﹣![]() x+5与直线y=kx+2互相垂直,则﹣
x+5与直线y=kx+2互相垂直,则﹣![]() k=﹣1.所以k=6
k=﹣1.所以k=6
解决问题
(1)请写出一条直线解析式______,使它与直线y=x﹣3平行.
(2)如图3,点A坐标为(﹣1,0),点P是直线y=﹣3x+2上一动点,当点P运动到何位置时,线段PA的长度最小?并求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一张长方形纸片,![]() (
(![]() ).将这张纸片沿着过点
).将这张纸片沿着过点![]() 的折痕翻折,使点
的折痕翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() ,折痕交
,折痕交![]() 于点
于点![]() ,将折叠后的纸片再次沿着另一条过点
,将折叠后的纸片再次沿着另一条过点![]() 的折痕翻折,点
的折痕翻折,点![]() 恰好与点
恰好与点![]() 重合,此时折痕交
重合,此时折痕交![]() 于点
于点![]() .
.
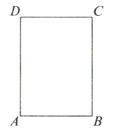
(1)在图中确定点![]() 、点
、点![]() 和点
和点![]() 的位置;
的位置;
(2)联结![]() ,则
,则![]() ______
______![]() ;
;
(3)用含有![]() 的代数式表示线段
的代数式表示线段![]() 的长.(注:直角三角形中,两直角边的平方的和等于斜边的平方)
的长.(注:直角三角形中,两直角边的平方的和等于斜边的平方)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知n边形的内角和θ=(n﹣2)×180°.
(1)甲同学说,θ能取900°;而乙同学说,θ也能取800°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了540°,用列方程的方法确定x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“食品安全”受到全社会的广泛关注,我市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有_________人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_________度;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
扇形统计图 条形统计图
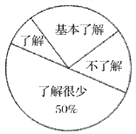
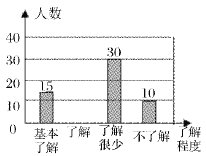
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿色出行是相对环保的出行方式,通过碳减排和碳中和实现环境资源的可持续利用和交通可持续发展.汽车工业的发展为人类带来了快捷和方便,但同时,汽车的发展也引起了能源的消耗和空气的污染.并且已成为全国各大城市的第一大污染源。实验中学为了解全校学生的交通方式,责成该校七年级(1班)的4位同学对该校部分学生进行了随机调查,按“骑自行车”、“乘公交车”、“步行”、“乘私家车”、“其他方式”设置选项.要求被调查的所有学生从中选一项,并将调查结果绘制成了条形统计图1和扇形统计图2.根据所提供的信息,解答下列问题.
(1)本次调查的人数共有___________人,扇形中步行的圆心角度度数为________.
(2)把条形统计图补充完整.
(3)若该校共有学生3000人,则全校步行的学生大约有多少人数?
(4)根据调查结果对学生的环保出行提一条合理化的建议.
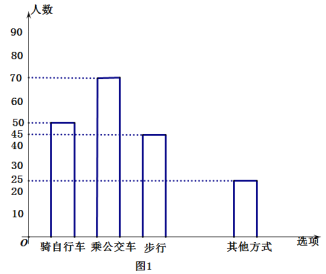
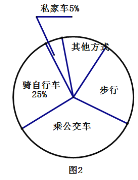
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
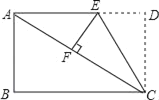
【题目】如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.
(1)求EF的长;
(2)求梯形ABCE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com