
【题目】如图1,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 点
点![]() ;点
;点![]() 在直线
在直线![]() 的右侧,且
的右侧,且![]() .
.

(1)若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标;
的坐标;
(2)如图2,若点![]() 在第四象限,且
在第四象限,且![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,求证:
,求证:![]() 是
是![]() 两个外角平分线的交点.
两个外角平分线的交点.
【答案】(1)P(4,2)或(2,﹣2);(2)证明见解析.
【解析】
(1)分两种情况,利用等腰三角形的性质,及全等三角形的性质求出PC,BC,即可得出结论;
(2)过点P作PC⊥x轴于C,PD⊥y轴于D,PE⊥MN于E.证明PC=PD=PE即可.
(1)A(﹣2,0),B(0,4),
∴OA=2,OB=4.
∵△ABP是直角三角形,且∠APB=45°,
∴只有∠ABP=90°或∠BAP=90°,
如图2.
①当∠ABP=90°时.
∵∠APB=∠BAP=45°,
∴AB=PB,
过点P作PC⊥OB于C,
∴∠BPC+∠CBP=90°.
∵∠CBP+∠ABO=90°,
∴∠ABO=∠BPC,
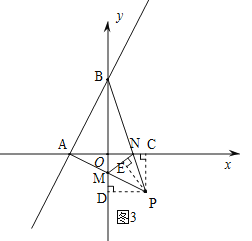
在△AOB和△BCP中,
∵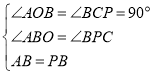 ,
,
∴△AOB≌△BCP(AAS),
∴PC=OB=4,BC=OA=2,
∴OC=OB﹣BC=2,
∴P(4,2),
②当∠BAP'=90°时,过点P'作P'D⊥OA于D.
同①的方法得:△ADP'≌△BOA,
∴DP'=OA=2,AD=OB=4,
∴OD=AD﹣OA=2,
∴P'(2,﹣2);
综上所述:满足条件的点P(4,2)或(2,﹣2);
(2)过点P作PC⊥x轴于C,PD⊥y轴于D,PE⊥MN于E.如图3,由(1)知点P(2,﹣2).
∵A(﹣2,0),
∴直线AP的解析式为y![]() x﹣1,
x﹣1,
∴M(0,﹣1),
∴BM=5,
同理:直线BP的解析式为y=﹣3x+4,
∴N(![]() ,0).
,0).
易求直线MN的解析式为![]() .
.
∵直线PE⊥直线MN,
∴直线PE的解析式为![]() ,即
,即![]() .
.
解方程组 ,得:
,得: ,
,
∴E(![]() ,
,![]() ),
),
∴PE=![]() =2.
=2.
∵P(2,﹣2),
∴PC=PD=2.
∵PD=PE,
∴P在∠DMN的平分线上.
∵PE=PC,
∴P在∠MNC的平分线上,
∴P是△OMN两个外角平分线的交点.




 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】为奖励优秀学生,某校准备购买一批文具袋和圆规作为奖品,已知购买1个文具袋和2个圆规需21元,购买2个文具袋和3个圆规需39元。
(1)求文具袋和圆规的单价。
(2)学校准备购买文具袋20个,圆规若干,文具店给出两种优惠方案:
方案一:购买一个文具袋还送1个圆规。
方案二:购买圆规10个以上时,超出10个的部分按原价的八折优惠,文具袋不打折.
①设购买面规m个,则选择方案一的总费用为______,选择方案二的总费用为______.
②若学校购买圆规100个,则选择哪种方案更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
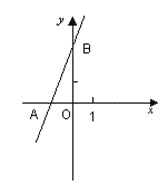
(1)求A,B两点的坐标;
(2)过B点作直线BP与x轴相交于P,且使OP=2OA, 求ΔABP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至![]() ,旋转角为
,旋转角为![]() .
.

(1)当点![]() 恰好落在EF边上时,求旋转角
恰好落在EF边上时,求旋转角![]() 的值;
的值;
(2)如图2,G为BC的中点,且00<![]() <900,求证:
<900,求证:![]() ;
;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,![]() 与
与![]() 能否全等?若能,直接写出旋转角
能否全等?若能,直接写出旋转角![]() 的值;若不能,说明理由.
的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).
根据图象提供的信息,解答下列问题:

(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究
小聪将命题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.
小聪的探究方法是对∠B分为“直角、钝角、锐角”三种情况进行探究.
第一种情况:当∠B 是直角时,如图1,△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据“HL”定理,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B 是锐角时,如图2,BC=EF,∠B=∠E<90°,在射线EM上有点D,使DF=AC,画出符合条件的点D,则△ABC和△DEF的关系是 ;
A.全等 B.不全等 C.不一定全等
第三种情况:当∠B是钝角时,如图3,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E>90°.过点C作AB边的垂线交AB延长线于点M;同理过点F作DE边的垂线交DE延长线于N,根据“ASA”,可以知道△CBM≌△FEN,请补全图形,进而证出△ABC≌△DEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京张高铁是2022年北京冬奥会的重要交通保障设施.如图,京张高铁起自北京北站,途经清河、沙河、昌平等站,终点站为张家口南站,全长174千米.根据资料显示,京张高铁在某次测试中的平均时速是现运行的京张铁路某![]() 字头列车平均时速的6倍,全程行驶时间减少了122分钟,且每站(不计起始站和终点站)停靠的平均时间也减少了3.5分钟.请求出此次测试中京张高铁的平均时速是多少.
字头列车平均时速的6倍,全程行驶时间减少了122分钟,且每站(不计起始站和终点站)停靠的平均时间也减少了3.5分钟.请求出此次测试中京张高铁的平均时速是多少.
(注:平均时速的测算公式为![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生体育课上蓝球运球的掌握情况,随机抽取部分八年级学生蓝球运球的测试成绩,按![]() ,
,![]() ,
,![]() ,
,![]() 四个等级进行统计,制成了如图所示的不完整的统计图
四个等级进行统计,制成了如图所示的不完整的统计图
根据所给信息,解答以下问题

(1)在扇形统计图中,求![]() 等级对应的扇形圆心角的度数,并补全条形统计图
等级对应的扇形圆心角的度数,并补全条形统计图
(2)该校八年级有![]() 名学生,请估计蓝球运球测试成绩达到
名学生,请估计蓝球运球测试成绩达到![]() 等级的学生
等级的学生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AC=BC,点D,E分别在边AB, BC 上,把△BDE沿直线DE翻折,使点B落在点B'处,DB',EB'分别交AC于点F,G,若∠ADF=80°,则∠EGC的大小为( ).

A.60°B.70°
C.80°D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com