
【题目】某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).
根据图象提供的信息,解答下列问题:

(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润为多少万元?
【答案】(1) ![]() ;(2) 截止到10月末,公司累积利润可达到30万元;(3) 第8个月公司获利润5.5万元.
;(2) 截止到10月末,公司累积利润可达到30万元;(3) 第8个月公司获利润5.5万元.
【解析】试题分析:
(1)由图可知:函数图象经过了点(1,-1.5)、点(2,-2)和点(5,2.5),设解析式为![]() ,代入三点的坐标,列出方程组,就可求得
,代入三点的坐标,列出方程组,就可求得![]() 的值,从而得的解析式;
的值,从而得的解析式;
(2)把![]() 代入(1)中所求得的解析式,解出
代入(1)中所求得的解析式,解出![]() 的值,并结合实际意义可得答案;
的值,并结合实际意义可得答案;
(3)把![]() 分别代入(1)中所得的解析式,求出对应的
分别代入(1)中所得的解析式,求出对应的![]() 的值,用
的值,用![]() 可得8月份的利润;
可得8月份的利润;
试题解析:
解:(1)设s与t的函数关系式为s=at2+bt+c,图象上三点坐标分别为
(1,-1.5),(2,-2),(5,2.5).分别代入,得
∴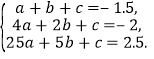 解得
解得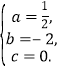 ,
,
∴![]()
(2)把s=30代入![]()
解得t1=10,t2=-6(舍去).
即截止到10月末,公司累积利润可达到30万元.
(3)把t=7代入![]() 得7月末的累积利润为s7=10.5(万元).
得7月末的累积利润为s7=10.5(万元).
把t=8代入![]() 得8月末的累积利润为s8=16(万元).
得8月末的累积利润为s8=16(万元).
∴s8-s7=16-10.5=5.5(万元).
即第8个月公司获利润5.5万元.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点 A 是反比例函数 y ![]() 在第一象限图象上的一个动点,连接 OA,以
在第一象限图象上的一个动点,连接 OA,以![]() OA 为长,OA为宽作矩形 AOCB,且点 C 在第四象限,随着点 A 的运动,点 C 也随之运动,但点 C 始终在反比例函数 y
OA 为长,OA为宽作矩形 AOCB,且点 C 在第四象限,随着点 A 的运动,点 C 也随之运动,但点 C 始终在反比例函数 y ![]() 的图象上,则 k 的值为________.
的图象上,则 k 的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图:
(1)画一条线段MN,使MN=![]() ;
;
(2)画△ABC,三边长分别为3,![]() ,
,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )

A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=kx2+(2k-1)x-1与x轴交点的横坐标为x1,x2(x1<x2),则对于下列结论:(1) 当x= -2时,y=1;(2) 当x> x2时,y>0;(3)方程kx2+(2k-1)x-1=0有两个不相等的实数根x1,x2;(4) x1<-1,x2>-1;(5) x2 -x1 = ![]() ,其中正确的结论有_______(只需填写序号)
,其中正确的结论有_______(只需填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xoy 中,已知点 A 的坐标为(-2,0).
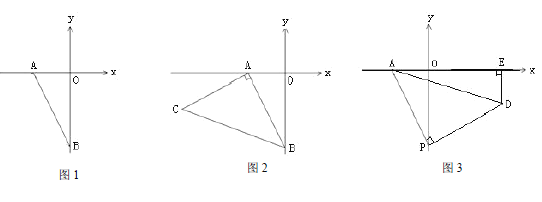
(1)如图 1,当点 B 的坐标为(0,-4)时,则△AOB 的面积是 ;
(2)如图 2,在(1)的条件下,过点 A 作 AC⊥AB,且使 AC=AB,求第三象限内的点 C 的坐标;
(3)如图 3,P 为 y 轴负半轴上一点,过点 P 作 PD⊥PA,且使 PD=PA,过第四象限内的点 D 作 DE⊥x 轴于 E,试判断 OP-DE 的值是否发生变化.若不发生变化,请求其值;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,点A,E,B,C不在同一条直线上.

(1)如图1,求证:∠E+∠C﹣∠A=180°
(2)如图2.直线FA,CP交于点P,且∠BAF=![]() ∠BAE,∠DCP=
∠BAE,∠DCP=![]() ∠DCE.
∠DCE.
①试探究∠E与∠P的数量关系;
②如图3,延长CE交PA于点Q,若AE∥PC,∠BAQ=α(0°<α<22.5°),则∠PQC的度数为 (用含α的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市现在有两种用电收费方法:
分时电表 | 普通电表 | |
峰时(8:00~21:00) | 谷时(21:00到次日8:00) | |
电价0.55元/千瓦·时 | 电价0.35元/千瓦·时 | 电价0.52元/千瓦·时 |
小明家所在的小区用的电表都换成了分时电表.
解决问题:
(1)小明家庭某月用电总量为![]() 千瓦·时(
千瓦·时(![]() 为常数);谷时用电
为常数);谷时用电![]() 千瓦·时,峰时用电
千瓦·时,峰时用电![]() 千瓦·时,分时计价时总价为
千瓦·时,分时计价时总价为![]() 元,普通计价时总价为
元,普通计价时总价为![]() 元,求
元,求![]() ,
,![]() 与用电量的函数关系式.
与用电量的函数关系式.
(2)小明家庭使用分时电表是不是一定比普通电表合算呢?
(3)下表是路皓家最近两个月用电的收据:
谷时用电(千瓦·时) | 峰时用电(千瓦·时) |
181 | 239 |
根据上表,请问用分时电表是否合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com