
����Ŀ��ij�������������õ��շѷ�����
��ʱ��� | ��ͨ��� | |
��ʱ��8:00��21:00�� | ��ʱ��21:00������8:00�� | |
���0.55Ԫ/ǧ�ߡ�ʱ | ���0.35Ԫ/ǧ�ߡ�ʱ | ���0.52Ԫ/ǧ�ߡ�ʱ |
С�������ڵ�С���õĵ���������˷�ʱ���.
������⣺
��1��С����ͥij���õ�����Ϊ![]() ǧ�ߡ�ʱ��
ǧ�ߡ�ʱ��![]() Ϊ����������ʱ�õ�
Ϊ����������ʱ�õ�![]() ǧ�ߡ�ʱ����ʱ�õ�
ǧ�ߡ�ʱ����ʱ�õ�![]() ǧ�ߡ�ʱ����ʱ�Ƽ�ʱ�ܼ�Ϊ
ǧ�ߡ�ʱ����ʱ�Ƽ�ʱ�ܼ�Ϊ![]() Ԫ����ͨ�Ƽ�ʱ�ܼ�Ϊ
Ԫ����ͨ�Ƽ�ʱ�ܼ�Ϊ![]() Ԫ����
Ԫ����![]() ��
��![]() ���õ����ĺ�����ϵʽ.
���õ����ĺ�����ϵʽ.
��2��С����ͥʹ�÷�ʱ����Dz���һ������ͨ��������أ�
��3���±���·������������õ���վݣ�
��ʱ�õ磨ǧ�ߡ�ʱ�� | ��ʱ�õ磨ǧ�ߡ�ʱ�� |
181 | 239 |
�����ϱ��������÷�ʱ����Ƿ���㣿
���𰸡���1��y1=0.35x+0.55��a-x����y2=0.52a����2����x��![]() ʱ��ʹ�÷�ʱ�������ͨ������㣻��x=
ʱ��ʹ�÷�ʱ�������ͨ������㣻��x=![]() ʱ�����ֵ��������ͬ����x��
ʱ�����ֵ��������ͬ����x��![]() ʱ��ʹ����ͨ�������ͨ������㣻��3���÷�ʱ���������.
ʱ��ʹ����ͨ�������ͨ������㣻��3���÷�ʱ���������.
��������
��1�����������ɣ�
��2�����������в���ʽ��ɣ�
��3�����ݣ�1���Ľ��۽�ɣ�
�⣺��1����������ã�y1=0.35x+0.55��a-x����y2=0.52a��
��2��С����ͥʹ�÷�ʱ�����һ������ͨ������㣮
��y1��y2����0.35x+0.55��a-x����0.52a�����x��![]() ��
��
��x��![]() ʱ��ʹ�÷�ʱ�������ͨ������㣻
ʱ��ʹ�÷�ʱ�������ͨ������㣻
��y1=y2����0.35x+0.55��a-x��=0.52a�����x=![]() ��
��
��x=![]() ʱ�����ֵ��������ͬ��
ʱ�����ֵ��������ͬ��
��y1��y2����0.35x+0.55��a-x����0.52a�����x��![]() ��
��
��x��![]() ʱ��ʹ����ͨ�������ͨ������㣻
ʱ��ʹ����ͨ�������ͨ������㣻
��3���÷�ʱ����ķ���Ϊ��0.35��181+0.55��239=194.8��Ԫ����
ʹ����ͨ����ķ���Ϊ��0.52����181+239��=218.4��Ԫ����
�����÷�ʱ��������㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�Ƴ���һ�ָ�Ч������ϴ����Ʒ��������к�˾�����˴ӿ���ӯ���Ĺ��̣�����Ķ��κ���ͼ��(����)�̻��˸ù�˾��������ۻ�����s(��Ԫ)������ʱ��t(��)֮��Ĺ�ϵ(��ǰt���µ������ܺ�s��t֮��Ĺ�ϵ)��
����ͼ���ṩ����Ϣ������������⣺

(1)����֪ͼ���ϵ��������꣬���ۻ�����s(��Ԫ)��ʱ��t(��)֮��ĺ�����ϵʽ��
(2)���ֹ������ĩ��˾�ۻ�����ɴﵽ30��Ԫ��
(3)���8���¹�˾��������Ϊ������Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ����4���㣺A��0��2����B����2����2����C����2��2����D��3��3����
��1���������������л�����ABC�����Բ��M��Բ��M���������� ����
��2����EF�ǡ�M��һ����Ϊ4���ң���GΪ��EF���е㣬��DG�����ֵ��
��3����P��ֱ��MB�ϣ�����M�ϴ���һ��Q��ʹ��P��Q��������С��1��ֱ��д����P�������ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�������������У�ÿһ��С�����εı߳�Ϊ1����ABC���������㶼�ڸ���ϣ�A��C������ֱ���(��4��6)��(��1��4)��
(1)����ͼ�е�����ƽ���ڽ���ƽ��ֱ������ϵ��
(2)�뻭����ABC����ƽ��6����λ����A1B1C1����д��C1�������� ����
(3)�뻭����ABC����ԭ��O�ԳƵ���A2B2C2 �� ��д����C2�������� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������������ֱ��A��B����ͬʱ�ظ��ٹ�·ʻ��C�ǣ���֪A��C���ǵ�·��Ϊ500ǧ�ף�B��C���ǵ�·��Ϊ450ǧ�ף��׳����ҳ����ٶȿ�10ǧ�ף�ʱ�����������ͬʱ����C�ǣ����������ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�A��BΪx�������㣬C��DΪy���ϵ����㣬��
�У�A��BΪx�������㣬C��DΪy���ϵ����㣬��
����A��C��B�������ߵ�һ����C1�뾭����A��D��B�������ߵ�һ����C2��ϳ�һ��������ߣ����ǰ�������
�����߳�Ϊ�����ߡ�����֪��C������Ϊ��0��![]() ������M��������C2��
������M��������C2��![]() ��
��![]() ��0���Ķ��㣮
��0���Ķ��㣮

��1����A��B��������ꣻ
��2�������ߡ��ڵ����������Ƿ����һ��P��ʹ����PBC�������������ڣ������PBC��������ֵ���������ڣ���˵�����ɣ�
��3������BDMΪֱ��������ʱ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ������ ��
A����������״����С���ʵ���ȫһ����5�������1��������������һ����һ���Ǻ���
B������Ԥ�������콵ˮ����10%������ָ������10%��ʱ�������
C��ij�ط���һ�ָ�����Ʊ���н�����ǧ��֮һ����ô�������ֲ�Ʊ1000�ţ�һ�����н�
D��������һö����Ӳ�ң���5�ζ������泯�ϣ����������Ȼ�������泯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
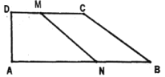
����Ŀ����ͼ����ֱ������ABCD�У�DC��AB����A=90����AB=26cm��DC=18cm ��AD=4cm������M��1cm/s���ٶȴӵ�D���C�˶�������N�ӵ�B��2cm/s���ٶ����A�˶���M��Nͬʱ������������һ�����㵽��˵�ʱֹͣ�˶�����һ������Ҳ��ֹ֮ͣ�˶����趯���˶�ʱ��Ϊt(s)���ı���ANMD�����y(![]() )��y����x�ĺ�������ʽ��д��������_____.
)��y����x�ĺ�������ʽ��д��������_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC�ա�EDC��
��1����DE��BC����ͼ1�����жϡ�ABC����״��˵�����ɣ�
��2������BE����AC��F����H��CE�ϵĵ㣬��CH=CF������DH��BE��K����ͼ2������֤����DKF=��ACB

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com